题目内容
已知函数f(x)=ex-x-1(e为自然对数的底数,e=2.71828…)
(1)判断函数f(x)的零点个数,并说明理由;
(2)已知n∈N*,且An+Bn=
f(x)dx+n,An是等差数列{an}的前n项和,Bn是首项为e-1的等比数列{bn}的前n项和,请求出数列{an},{bn}的通项公式;
(3)若{x|f(x)>ax-1}∩{x|
≤x≤2}=∅,求实数a的取值范围.
(1)判断函数f(x)的零点个数,并说明理由;
(2)已知n∈N*,且An+Bn=
| ∫ | n 0 |
(3)若{x|f(x)>ax-1}∩{x|
| 1 |
| 2 |
考点:数列的应用,函数零点的判定定理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)求导数,确定函数的单调性,可得最小值,即可确定函数f(x)的零点个数;
(2)利用定积分,可得An+Bn=-
n2+en-1,由等差数列、等比数列的前n项和性质可得结论;
(3)x∈[
,2]时,f(x)>ax-1等价于ex-x>ax,即a<
,求出右边的最大值,即可得出结论.
(2)利用定积分,可得An+Bn=-
| 1 |
| 2 |
(3)x∈[
| 1 |
| 2 |
| ex-x |
| x |
解答:
解:(1)∵f(x)=ex-x-1,
∴f′(x)=ex-1,
∴x<0,f′(x)<0,x>0,f′(x)>0,
∴f(x)min=f(0)=0,
∴x≠0时,f(x)>0,故f(x)只有一个零点;
(2)∵An+Bn=
f(x)dx+n,
∴An+Bn=-
n2+en-1,
由等差数列、等比数列的前n项和性质可知:An=-
n2,Bn=en-1,
∴an=-n+
,bn=(e-1)en-1;
(3)x∈[
,2]时,f(x)>ax-1等价于ex-x>ax,即a<
,
设g(x)=
,则g′(x)=
,
x>1时,g′(x)>0;x<1时,g′(x)<0,
∵g(
)=2
-1,g(2)=
-1,
∴x∈[
,2]时,g(x)max=g(2)=
-1,
∴a<
-1,即a的取值范围为(-∞,
-1).
∴f′(x)=ex-1,
∴x<0,f′(x)<0,x>0,f′(x)>0,
∴f(x)min=f(0)=0,
∴x≠0时,f(x)>0,故f(x)只有一个零点;
(2)∵An+Bn=
| ∫ | n 0 |
∴An+Bn=-
| 1 |
| 2 |
由等差数列、等比数列的前n项和性质可知:An=-
| 1 |
| 2 |
∴an=-n+
| 1 |
| 2 |
(3)x∈[
| 1 |
| 2 |
| ex-x |
| x |
设g(x)=
| ex-x |
| x |
| ex(x-1) |
| x2 |
x>1时,g′(x)>0;x<1时,g′(x)<0,
∵g(
| 1 |
| 2 |
| e |
| e2 |
| 2 |
∴x∈[
| 1 |
| 2 |
| e2 |
| 2 |
∴a<
| e2 |
| 2 |
| e2 |
| 2 |
点评:本题考查数列与函数的综合,考查导数知识,考查函数的单调性,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
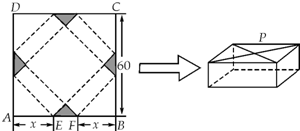 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为