题目内容
已知三棱锥P-ABC的顶点都在同一球面上,PA⊥平面ABC,∠ABC=150°,PA=1,AC=2,则该球的表面积为 .
考点:球的体积和表面积
专题:球
分析:通过底面三角形ABC求出底面圆的半径AM,判断球心到底面圆的距离OM,求出半径,即可求解取得表面积.
解答:
 解:△ABC中,∠ABC=150°,AC=2,底面三角形的底面半径为:
解:△ABC中,∠ABC=150°,AC=2,底面三角形的底面半径为:
AM=
=2,AP是球的弦,PA=1,∴OM=
AP=
,
∴球的半径OA=
=
.
该球的表面积为:4πOA2=17π.
故答案为:17π.
 解:△ABC中,∠ABC=150°,AC=2,底面三角形的底面半径为:
解:△ABC中,∠ABC=150°,AC=2,底面三角形的底面半径为:AM=
| AC |
| 2sin∠ABC |
| 1 |
| 2 |
| 1 |
| 2 |
∴球的半径OA=
22+(
|
| ||
| 2 |
该球的表面积为:4πOA2=17π.
故答案为:17π.
点评:本题考查球的表面积的求法,球的内接体,考查空间想象能力以及计算能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
已知向量
=(1,cosα),
=(2,1)且
∥
,则锐角α的大小为( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知偶函数f(x)对任意x∈R都有f(x+4)-f(x)=2f(2),则f(2014)的值等于( )
| A、2 | B、3 | C、4 | D、0 |
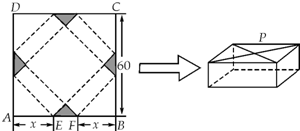 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为