题目内容
已知直线x+y+1=0与曲线C:y=x3-3px2相交于点A,B,且曲线C在A,B处的切线平行,则实数p的值为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,设出A,B点的坐标,得到函数在A,B点处的导数值,由A,B点处的导数值相等得到3x12-6px1=3x22-6px2=m,把x1,x2看作方程3x2-6px-m=0的两个根,利用根与系数关系得到x1+x2=2p,进一步得到AB的中点坐标,然后再证明AB的中点在曲线C上,最后由AB中点的纵坐标相等求得实数p的值.
解答:
解:由y=x3-3px2,得y′=3x2-6px,
设A(x1,y1),B(x2,y2),
则曲线C在A,B处的切线的斜率分别为3x12-6px1,3x22-6px2,
∵曲线C在A,B处的切线平行,
∴3x12-6px1=3x22-6px2,
令3x12-6px1=3x22-6px2=m,
∴x1,x2是方程3x2-6px-m=0的两个根,
则x1+x2=2p,
下面证线段AB的中点在曲线C上,
∵
=
=
=-2p3,
而(
)3-3p(
)2=(
)3-3p(
)2=-2p3,
∴线段AB的中点在曲线C上,
由x1+x2=2p,知线段的中点为(p,-p-1),
∴-p-1=p3-3p•p2=-2p3,解得p=1.
故答案为:1.
设A(x1,y1),B(x2,y2),
则曲线C在A,B处的切线的斜率分别为3x12-6px1,3x22-6px2,
∵曲线C在A,B处的切线平行,
∴3x12-6px1=3x22-6px2,
令3x12-6px1=3x22-6px2=m,
∴x1,x2是方程3x2-6px-m=0的两个根,
则x1+x2=2p,
下面证线段AB的中点在曲线C上,
∵
| x13-3px12+x23-3px22 |
| 2 |
| (x1+x2)[(x1+x2)2-3x1x2]-3p[(x1+x2)2-2x1x2] |
| 2 |
=
| 8p3-12p3 |
| 2 |
而(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 2p |
| 2 |
| 2p |
| 2 |
∴线段AB的中点在曲线C上,
由x1+x2=2p,知线段的中点为(p,-p-1),
∴-p-1=p3-3p•p2=-2p3,解得p=1.
故答案为:1.
点评:本题考查利用导数研究曲线上某点的切线方程,求解该题的主线是利用AB中点的坐标相等,关键是证明AB的中点在曲线C上,是中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知集合A={x|x<3},B={x|log2x<2},则A∩B=( )
| A、(-1,3) |
| B、(0,4) |
| C、(0,3) |
| D、(-1,4) |
已知x,y∈R,则(x2+
)(
+4y2)的最小值为( )
| 1 |
| y2 |
| 1 |
| x2 |
| A、10 | B、8 | C、9 | D、7 |
命题“?x∈R,x2-x-1≥0恒成立”的否定是( )
| A、?x∈R,x2-x-1<0恒成立 |
| B、?x∈R,x2-x-1≤0恒成立 |
| C、?x∈R,x2-x-1≥0成立 |
| D、?x∈R,x2-x-1<0恒成立. |
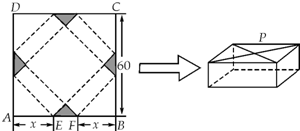 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为