题目内容
在数列{an}中,a1=3,(an+1-2)(an-2)=2(n∈N*),则该数列的前2014项的和是 .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出
=1,从而得到数列{an}是一个周期为2的周期数列,由此能求出S2014.
| an+1-2 |
| an-1-2 |
解答:
解:在数列{an}中,∵a1=3,(an+1-2)(an-2)=2(n∈N*),
∴(an-2)(an-1-2)=2,n∈N*,n≥2,
以上两式相除,得
=1,
∴an+1-2=an-1-2,n∈N*,n≥2,
∴数列{an}是一个周期为2的周期数列,
∵a2-2=
,a1=3,∴a2=4,
∴S2014=1007×(a1+a2)=1007×(3+4)=7049.
故答案为:7049.
∴(an-2)(an-1-2)=2,n∈N*,n≥2,
以上两式相除,得
| an+1-2 |
| an-1-2 |
∴an+1-2=an-1-2,n∈N*,n≥2,
∴数列{an}是一个周期为2的周期数列,
∵a2-2=
| 2 |
| a1-2 |
∴S2014=1007×(a1+a2)=1007×(3+4)=7049.
故答案为:7049.
点评:本题考查数列的前2014项的和的求法,是中档题,解题时要关键是判断出数列{an}是一个周期为2的周期数列.

练习册系列答案
相关题目
已知函数y=f(x)(x∈N*),f(1)=1,f(n)=(-1)n•3f(n-1)(n≥2),则f(4)等于( )
| A、27 | B、-27 | C、9 | D、-9 |
已知偶函数f(x)对任意x∈R都有f(x+4)-f(x)=2f(2),则f(2014)的值等于( )
| A、2 | B、3 | C、4 | D、0 |
把二进制数10011(2)转化为十进制数是( )
| A、19 | B、18 | C、17 | D、16 |
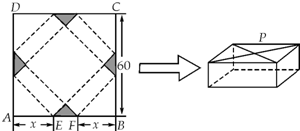 如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为
如图,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的一个等腰直角三角形斜边的两个端点.设AE=FB=xcm.若要使包装盒的侧面积最大,则x的值为