题目内容
已知f(x)=ln(1-x)-ln(1+x).
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性,并证明;
(3)用定义证明函数f(x)在定义域内单调递减.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性,并证明;
(3)用定义证明函数f(x)在定义域内单调递减.
考点:对数函数的图像与性质,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)求函数f(x)的定义域,可令1-x>0且1+x>0,解出此不等式的解集即可得到所求函数的定义域;
(2)判断函数的奇偶性,要用定义法,由函数解析式研究f(-x)与f(x)的关系,即可证明出函数的性质;
(3)此函数是一个减函数,由定义法证明要先任取x1,x2∈(-1,1)且x1<x2,再两函数值作差,判断差的符号,再由定义得出结论.
(2)判断函数的奇偶性,要用定义法,由函数解析式研究f(-x)与f(x)的关系,即可证明出函数的性质;
(3)此函数是一个减函数,由定义法证明要先任取x1,x2∈(-1,1)且x1<x2,再两函数值作差,判断差的符号,再由定义得出结论.
解答:
解:(1)由题意令1-x>0且1+x>0,
解得-1<x<1,所以函数的定义域是(-1,1)
(2)此函数是一个奇函数,证明如下:
由(1)知函数的定义域关于原点对称,
f(x)=ln(1-x)-ln(1+x)=ln
,
则f(-x)=ln
=-ln
=-f(x),故函数是奇函数;
(3)此函数在定义域上是减函数,证明如下:
任取x1,x2∈(-1,1)且x1<x2,f(x1)-f(x2)=ln
-ln
=ln
,
由于x1,x2∈(-1,1)且x1<x2,
∴1-x1>1-x2>0,1+x2>1+x1>0,可得
>1,
所以ln
>0,
即有f(x1)-f(x2)>0,即f(x1)>f(x2)
故函数在定义域是减函数
解得-1<x<1,所以函数的定义域是(-1,1)
(2)此函数是一个奇函数,证明如下:
由(1)知函数的定义域关于原点对称,
f(x)=ln(1-x)-ln(1+x)=ln
| 1-x |
| 1+x |
则f(-x)=ln
| 1+x |
| 1-x |
| 1-x |
| 1+x |
(3)此函数在定义域上是减函数,证明如下:
任取x1,x2∈(-1,1)且x1<x2,f(x1)-f(x2)=ln
| 1-x1 |
| 1+x1 |
| 1-x2 |
| 1+x2 |
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
由于x1,x2∈(-1,1)且x1<x2,
∴1-x1>1-x2>0,1+x2>1+x1>0,可得
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
所以ln
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
即有f(x1)-f(x2)>0,即f(x1)>f(x2)
故函数在定义域是减函数
点评:本题考查了求函数的定义域,对数的运算法则,判断函数的奇偶性,定义法证明函数单调性,正确解答本题,关键是熟练记忆函数的性质及这些性质判断的方法,其中判断函数的单调性是本题的难点,定义法判断函数的单调性,其步骤是;取,作差,判号,得出结论,其中判号这一步易疏漏,切记

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知函数f(x)=
,则下列说法正确的是( )
| x-1 |
| x+2 |
| A、f(x)在R上为增函数 |
| B、f(x)在(-∞,-2)上为减函数,在(-2,+∞)上也为减函数 |
| C、f(x)在(-∞,-2)上为减函数,在(-2,+∞)上为增函数 |
| D、f(x)在(-∞,-2)上为增函数,在(-2,+∞)上为增函数 |
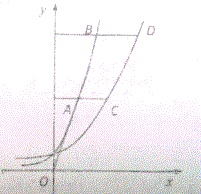 如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点.
如图,A,B是函数y=e2x的图象上两点,分别过A B作x轴的平行线与函数y=ex的图象交于C,D两点. 给出数表:请在其中找出5个不同的数,使它们由小到大能构成等比数列,则这5个数依次可以说是
给出数表:请在其中找出5个不同的数,使它们由小到大能构成等比数列,则这5个数依次可以说是