Question

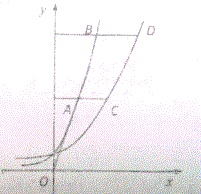如图，A，B是函数y=e^2x的图象上两点，分别过A B作x轴的平行线与函数y=e^x的图象交于C，D两点．
（1）求点A与原点O连成直线的斜率取值范围；
（2）若直线AB过原点O，求证直线CD也过原点O；
（3）当直线BC与y轴平行时，设B点的横坐标为x，四边形ABCD的面积为f（x），若方程2f（x）-3e^x=0在区间[t，t+1]上有实数解，求整数t的值．

Answer 1

考点：指数函数综合题

专题：导数的概念及应用,导数的综合应用

分析：（1）设过原点O且和函数y=e^2x的图象相切的切线的切点为P（a，b），求出切线斜率，可得点A与原点O连成直线的斜率取值范围；
（2）设A，B，C，D各点坐标为（x₁，y₁），（x₂，y₂），（x₃，y₁），（x₄，y₂）则y₁=e2x1=ex3，y₂=e2x2=ex4，即2x₁=x₃，2x₂=x₄，由直线AB过原点O，可得直线OA与OB斜率相等，进而可得直线OC，OD斜率也相等，得到结论；
（3）方程2f（x）-3e^x=0可化为：

3x

2

（e^x-1）e^x-3e^x=0，即e^x-

2

x

-1=0，构造函数g（x）=e^x-

2

x

-1，利用导数法判断单调性后，可得g（x）=e^x-

2

x

-1在[1，2]和[-3，-2]上各有一个零点，即方程2f（x）-3e^x=0在区间[1，2]和[-3，-2]上有实数解，进而可得整数t的值．

解答： 解：（1）设过原点O且和函数y=e^2x的图象相切的切线的切点为P（a，b），
则b=e^2a，又y′=2e^2x，
故切线OP的斜率k_OP=2e^2a，
解

e2a

a

=2e2a，得a=

1

2

，
故k_OP=2e，
故点A与原点O连成直线的斜率取值范围为（-∞，0）（0，2e）
（2）由已知可设A，B，C，D各点坐标为（x₁，y₁），（x₂，y₂），（x₃，y₁），（x₄，y₂）
则y₁=e2x1=ex3，y₂=e2x2=ex4，
即2x₁=x₃，2x₂=x₄，
∵直线AB过原点O，
∴

y2

x2

=

y1

x1

，
∴

y2

2x2

=

y1

2x1

，
即

y2

x4

=

y1

x3

，
即k_OC=k_OD，
∴直线CD也过原点O；
（3）当直线BC与y轴平行时，x₂=x₃=2x₁=x，2x₂=x₄=4x₁=2x，
∴f（x）=

1

2

[（x₃-x₁）+（x₄-x₂）]（y₂-y₁）=

3x

4

（e^x-1）e^x，
∴2f（x）-3e^x=0可化为：

3x

2

（e^x-1）e^x-3e^x=0，
由e^x＞0，且x=0不是该方程的解，故原方程等价于：e^x-

2

x

-1=0，
令g（x）=e^x-

2

x

-1，
则g′（x）=e^x+

2

x2

＞0恒成立，
故g（x）=e^x-

2

x

-1在（-∞，0）和（0，+∞）上均为增函数，
又由g（1）=e-3＜0，g（2）=e²-2＞0，
g（-3）=e^-3-

1

3

＜0，g（-2）=e^-2＞0，
故g（x）=e^x-

2

x

-1在[1，2]和[-3，-2]上各有一个零点，
即方程2f（x）-3e^x=0在区间[1，2]和[-3，-2]上有实数解，
故t=1，或t=-3

点评：本题考查的知识点是直线的斜率，三点共线的证明，函数的零点与方程根的关系，是函数，方程，导数与解析几何的综合应用，难度较大，属于难题．