题目内容
12.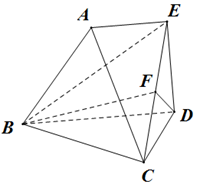 如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.
如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.(Ⅰ)求证:BF⊥CD;
(Ⅱ)求二面角C-BF-D的余弦值.
分析 (Ⅰ)取BD中点O,连接OC,OA,由题意可证OC、OD、OA两两互相垂直.以O为坐标原点,分别以OC、OD、OA所在直线为x、y、z轴建立空间直角坐标系,求出B,C,D,E,F的坐标,得到$\overrightarrow{BF}、\overrightarrow{CD}$的坐标,由$\overrightarrow{BF}•\overrightarrow{CD}=0$,可得$\overrightarrow{BF}⊥\overrightarrow{CD}$,即BF⊥CD;
(Ⅱ)分别求出平面BCF与平面BFD的一个法向量,利用两法向量所成角的余弦值可得二面角C-BF-D的余弦值.
解答 (Ⅰ)证明:如图,取BD中点O,连接OC,OA,
∵△BCD为正三角形,∴OC⊥BD,
∵面ABDE⊥面BCD,且面ABDE∩面BCD=BD,
∴OC⊥面ABDE,则OC⊥OA,
又AE∥DB,AE⊥DE,AE=$\frac{1}{2}DB$,
∴OA⊥OD.
以O为坐标原点,分别以OC、OD、OA所在直线为x、y、z轴建立空间直角坐标系,
则B(0,-1,0),C($\sqrt{3}$,0,0),D(0,1,0),E(0,1,1),F($\frac{\sqrt{3}}{2},\frac{1}{2},\frac{1}{2}$).
$\overrightarrow{BF}=(\frac{\sqrt{3}}{2},\frac{3}{2},\frac{1}{2})$,$\overrightarrow{CD}=(-\sqrt{3},1,0)$,
∵$\overrightarrow{BF}•\overrightarrow{CD}=-\frac{3}{2}+\frac{3}{2}=0$,∴$\overrightarrow{BF}⊥\overrightarrow{CD}$,即BF⊥CD;
(Ⅱ)解:$\overrightarrow{BF}=(\frac{\sqrt{3}}{2},\frac{3}{2},\frac{1}{2})$,$\overrightarrow{BC}=(\sqrt{3},1,0)$,$\overrightarrow{BD}=(0,2,0)$.
设平面BCF的一个法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BF}=0}\\{\overrightarrow{m}•\overrightarrow{BC}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}_{1}+\frac{3}{2}{y}_{1}+\frac{1}{2}{z}_{1}=0}\\{\sqrt{3}{x}_{1}+{y}_{1}=0}\end{array}\right.$,取x1=1,得$\overrightarrow{m}=(1,-\sqrt{3},2\sqrt{3})$.
设平面BFD的一个法向量$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BF}=0}\\{\overrightarrow{n}•\overrightarrow{BD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}_{2}+\frac{3}{2}{y}_{2}+\frac{1}{2}{z}_{2}=0}\\{2{y}_{2}=0}\end{array}\right.$,取x2=1,得$\overrightarrow{n}=(1,0,-\sqrt{3})$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1-6}{4×2}=-\frac{5}{8}$.
∴二面角C-BF-D的余弦值为$-\frac{5}{8}$.
点评 本题考查直线与平面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
| A. | $\frac{{3-4\sqrt{3}}}{10}$ | B. | $\frac{{3+4\sqrt{3}}}{10}$ | C. | $\frac{{-3-4\sqrt{3}}}{10}$ | D. | $\frac{{-3+4\sqrt{3}}}{10}$ |

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | y=$\sqrt{x}$ | B. | y=|sinx| | C. | y=ex-e-x | D. | y=cosx |