题目内容
20.设数列{an}的前n项和为${S_n}=2{n^2}-1$,数列{bn}的前n项和为Qn=2bn-2.(1)求数列{an}和{bn}的通项公式;
(2)设${c_n}=\frac{a_n}{b_n}$,求数列{cn}的前n项和Tn.
分析 (1)数列{an}的前n项和为${S_n}=2{n^2}-1$,可得n≥2时,an=Sn-Sn-1.n=1时,a1=S1=1.可得an.数列{bn}的前n项和为Qn=2bn-2.n≥2时,Qn-1=2bn-1-2,相减可得:bn=2bn-1.n=1时,b1=Q1=2b1-2,解得b1.利用等比数列的通项公式可得bn.
(2)${c_n}=\frac{a_n}{b_n}$,n=1时,c1=$\frac{1}{2}$,n≥2时,cn=$\frac{4n-2}{{2}^{n}}$=$\frac{2n-1}{{2}^{n-1}}$.利用错位相减法即可得出.
解答 解:(1)数列{an}的前n项和为${S_n}=2{n^2}-1$,
∴n≥2时,an=Sn-Sn-1=2n2-1-[2(n-1)2-1]=4n-2.
n=1时,a1=S1=1.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{4n-2,n≥2}\end{array}\right.$.
数列{bn}的前n项和为Qn=2bn-2.
n≥2时,Qn-1=2bn-1-2,可得bn=2bn-2bn-1,化为:bn=2bn-1.
n=1时,b1=Q1=2b1-2,解得b1=2.
∴数列{bn}是等比数列,首项与公比都为2.
∴bn=2n.
(2)${c_n}=\frac{a_n}{b_n}$,
n=1时,c1=$\frac{1}{2}$,n≥2时,cn=$\frac{4n-2}{{2}^{n}}$=$\frac{2n-1}{{2}^{n-1}}$.
∴n=1时,T1=c1=$\frac{1}{2}$.
n≥2时,Tn=$\frac{1}{2}+$$\frac{3}{2}$+$\frac{5}{{2}^{2}}$+…+$\frac{2n-1}{{2}^{n-1}}$.
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n-1}}$+$\frac{2n-1}{{2}^{n}}$.
∴$\frac{1}{2}{T}_{n}$=$\frac{7}{4}$+2×$(\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}})$-$\frac{2n-1}{{2}^{n}}$=$\frac{7}{4}$$+2×\frac{\frac{1}{4}[1-(\frac{1}{2})^{n-2}]}{1-\frac{1}{2}}$-$\frac{2n-1}{{2}^{n}}$.
∴Tn=$\frac{11}{2}$-$\frac{2n+3}{{2}^{n-1}}$.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、错位相减法、分类讨论方法,考查了推理能力与计算能力,属于中档题.

| A. | [5,+∞) | B. | (5,+∞) | C. | (-∞,5] | D. | (-∞,5) |
| A. | {x|0≤x≤4} | B. | {x|-1≤x≤4} | C. | {x|-1≤x≤0} | D. | {x|0<x≤4} |
| A. | $y=±\frac{1}{4}x$ | B. | $y=±\frac{1}{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | y=±x |
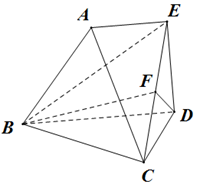 如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.
如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点.