题目内容
已知k∈{a|-1<a<1,且a≠0},设命题p:y=kx+2008的值随x的增大而增大;命题q:不等式x+|x-2k|>1的解集为R.p或q为真,p且q为假,求实数k的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先求出两个命题正确时k的范围,求出当p正确且q不正确时,0<k≤
,当p不正确且q正确时,k∈∅,求出满足条件的k的取值范围.
| 1 |
| 2 |
解答:
解:将已知条件转化为等价的简单不等式.首先研究q:
∵x+|x-2k|=
,
∴x+|x-2k|的最小值是2k.
∵x+|x-2k|>1的解集为R.
∴2k>1,k>
.
结合k∈{a|-1<a<1,a≠0}知
q正确时,
<k<1.q不正确时,-1<k≤
且k≠0,
其次研究p:y=kx+2008的值随x的增大而增大,
∴k>0.反之,k≤0,
∴p正确时,0<k<1,p不正确时,-1<k<0.
综上知,当p正确且q不正确时,0<k≤
,当p不正确且q正确时,k∈∅,
∴k的取值范围是0<k≤
.
∵x+|x-2k|=
|
∴x+|x-2k|的最小值是2k.
∵x+|x-2k|>1的解集为R.
∴2k>1,k>
| 1 |
| 2 |
结合k∈{a|-1<a<1,a≠0}知
q正确时,
| 1 |
| 2 |
| 1 |
| 2 |
其次研究p:y=kx+2008的值随x的增大而增大,
∴k>0.反之,k≤0,
∴p正确时,0<k<1,p不正确时,-1<k<0.
综上知,当p正确且q不正确时,0<k≤
| 1 |
| 2 |
∴k的取值范围是0<k≤
| 1 |
| 2 |
点评:本题主要考查了p或q型复合命题的真假判断的应用,解题的关键还是要能准确的求出命题P,命题q分别为真的范围.

练习册系列答案
相关题目
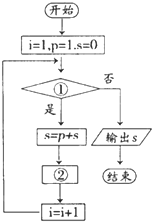 给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )
给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )| A、i≤16?; p=p+i-1 |
| B、i≤14?; p=p+i+1 |
| C、i≤15?; p=p+i+1 |
| D、i≤15?; p=p+i |
下列函数中与y=cosx奇偶性相同的是( )
| A、y=tanx |
| B、y=|sinx| |
| C、y=sinx |
| D、y=-sinx |
由正数组成的等比数列{an}满足:a4a8=9,则a5,a7的等比中项为( )
| A、±3 | B、3 | C、±9 | D、9 |
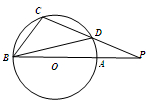 如图,AB是半径为3的⊙O的直径,CD是弦,BA,CD的延长线交于点P,PA=4,PD=5,则∠CBD=
如图,AB是半径为3的⊙O的直径,CD是弦,BA,CD的延长线交于点P,PA=4,PD=5,则∠CBD=