题目内容
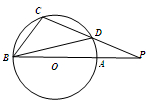如图，AB是半径为3的⊙O的直径，CD是弦，BA，CD的延长线交于点P，PA=4，PD=5，则∠CBD=考点：与圆有关的比例线段
专题：计算题,立体几何
分析：由圆的割线定理，PA•PB=PC•PD，可以求出PD=8，即CD=3，求∠CBD就是求弦CD所对应的圆周角的大小，那么问题就转化为求长为3的弦在半径为3的圆里所对应的圆周角．
解答：
解：由圆的割线定理，PA•PB=PC•PD，PA=4，PD=5，AB=6，
∴PC=8，
即CD=3，
∵CD=OC=3
∴弦CD所对应的圆心角是60°，
又由于同弧所对的圆心角等于圆周角的2倍，
∴弦CD对应的圆周角即是30°，
即∠CBD=30°．
故答案为：30°．
∴PC=8，
即CD=3，
∵CD=OC=3
∴弦CD所对应的圆心角是60°，
又由于同弧所对的圆心角等于圆周角的2倍，
∴弦CD对应的圆周角即是30°，
即∠CBD=30°．
故答案为：30°．
点评：本题考查和圆有关的比例线段，本题解题的关键是根据同弧所对的圆周角和圆心角之间的关系解题，本题是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
设f（n）=2+24+27+210+…+23n+1（n∈N），则f（n）等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
直线3x-4y-9=0与圆x2+y2=4的位置关系是（ ）
| A、相交但不过圆心 | B、相交且过圆心 |
| C、相切 | D、相离 |
某市为调研学校师生的环境保护意识，决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上（含80分）为达标．60所学校的考评结果频率分布直方图如图所示（其分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]）．