题目内容
已知将一枚质地不均匀的硬币抛掷三次,三次正面均朝上的概率为
.
(1)求抛掷这一枚质地不均匀的硬币三次,仅有一次正面朝上的概率;
(2)抛掷这一枚质地不均匀的硬币三次后,再抛掷另一枚质地均匀的硬币一次,记四次抛掷后正面朝上的总次数为ξ,求随机变量ξ的分布列及期望Eξ.
| 1 |
| 27 |
(1)求抛掷这一枚质地不均匀的硬币三次,仅有一次正面朝上的概率;
(2)抛掷这一枚质地不均匀的硬币三次后,再抛掷另一枚质地均匀的硬币一次,记四次抛掷后正面朝上的总次数为ξ,求随机变量ξ的分布列及期望Eξ.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(1)由硬币抛掷三次,三次正面均朝上的概率为
,设出掷一次这样的硬币,正面朝上的概率为r,由独立重复试验公式列出方程,解方程得到r的值.再由独立重复试验公式得到结果.
(2)抛掷一枚质地均匀的硬币四次抛掷后正面朝上的总次数为ξ,由题意知ξ的可能取值是0、1、2、3、4,根据独立重复试验公式得到结果,写出分布列,算出期望.
| 1 |
| 27 |
(2)抛掷一枚质地均匀的硬币四次抛掷后正面朝上的总次数为ξ,由题意知ξ的可能取值是0、1、2、3、4,根据独立重复试验公式得到结果,写出分布列,算出期望.
解答:
解:(1)设掷一次这样的硬币,正面朝上的概率为r,
则依题意有:
•r3=
.
可得r=
.
∴抛掷这一枚质地不均匀的硬币三次,仅有一次正面朝上的概率为
•
•(
)2=
;
(2)由题设知ξ的取值为0,1,2,3,4,
P(ξ=0)=
•(
)3•
=
,
P(ξ=1)=
•(
)3•
+
•
•(
)2•
=
,
P(ξ=2)=
•
•(
)2•
+
•(
)2•
•
=
,
P(ξ=3)=
•(
)2•
•
+
•(
)3•
=
,
P(ξ=4)=
•(
)3•
=
.
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
+3×
+4×
=
.
则依题意有:
| C | 3 3 |
| 1 |
| 27 |
可得r=
| 1 |
| 3 |
∴抛掷这一枚质地不均匀的硬币三次,仅有一次正面朝上的概率为
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
(2)由题设知ξ的取值为0,1,2,3,4,
P(ξ=0)=
| C | 0 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 27 |
P(ξ=1)=
| C | 0 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 10 |
| 27 |
P(ξ=2)=
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 9 |
| 27 |
P(ξ=3)=
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 54 |
P(ξ=4)=
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 54 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 4 |
| 27 |
| 10 |
| 27 |
| 9 |
| 27 |
| 7 |
| 54 |
| 1 |
| 54 |
| 3 |
| 2 |
点评:本题考查独立重复试验概率公式的运用,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
相关题目
直线xcosα+
y-2=0的倾斜角的取值范围是( )
| 3 |
A、[-
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[
|
函数f(x)=loga(x)在其定义域上是( )
| A、增函数 | B、减函数 |
| C、不是单调函数 | D、单调性与a有关 |
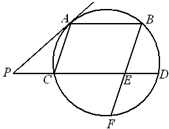 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.