题目内容
已知f(x)=x(
+k).
(1)当k=
时,判断函数f(x)的奇偶性;
(2)在(1)的条件下,证明f(x)>0;
(3)若对任意x∈[1,2]时,不等式f(x)>0恒成立,求k的取值范围.
| 1 |
| 2x-1 |
(1)当k=
| 1 |
| 2 |
(2)在(1)的条件下,证明f(x)>0;
(3)若对任意x∈[1,2]时,不等式f(x)>0恒成立,求k的取值范围.
考点:函数恒成立问题,函数单调性的性质,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用
分析:(1)根据函数的奇偶性的定义判断即可,
(2)根据指数函数的性质当x>0,可知2x-1>0,故得到f(x)>0,再根据函数为偶函数,继而得到f(x)>0恒成立;
(3)分离参数,得到k>
在[1,2]恒成立,构造函数g(x)=
,根据导数求出函数的最大值,问题得以解决.
(2)根据指数函数的性质当x>0,可知2x-1>0,故得到f(x)>0,再根据函数为偶函数,继而得到f(x)>0恒成立;
(3)分离参数,得到k>
| 1 |
| 1-2x |
| 1 |
| 1-2x |
解答:
解:(1)当k=
时,f(x)=x(
+
)=x
,
∵f(-x)=-x
=x
=f(x),
∴函数f(x)为偶函数,
(2)f(x)=x(
+
),
当x>0时,2x-1>0,
∴
+
>0,
∴f(x)=x(
+
)>0,
因为函数f(x)为偶函数,
故当x<0,f(x)>0,
综上所述f(x)>0恒成立,
(3)令f(x)>0,x∈[1,2],则x(
+k)>0,
即k>
在[1,2]恒成立,
设g(x)=
,
则g′(x)=
>0恒成立,
∴函数g(x)在[1,2]为增函数,
∴g(x)max=g(2)=
=-
,
∴k>-
故k的取值范围为(-
,+∞)
| 1 |
| 2 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
| 2x+1 |
| 2(2x-1) |
∵f(-x)=-x
| 2-x+1 |
| 2(2-x-1) |
| 2x+1 |
| 2(2x-1) |
∴函数f(x)为偶函数,
(2)f(x)=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
当x>0时,2x-1>0,
∴
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴f(x)=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
因为函数f(x)为偶函数,
故当x<0,f(x)>0,
综上所述f(x)>0恒成立,
(3)令f(x)>0,x∈[1,2],则x(
| 1 |
| 2x-1 |
即k>
| 1 |
| 1-2x |
设g(x)=
| 1 |
| 1-2x |
则g′(x)=
| 2xln2 |
| (1-2x)2 |
∴函数g(x)在[1,2]为增函数,
∴g(x)max=g(2)=
| 1 |
| 1-22 |
| 1 |
| 3 |
∴k>-
| 1 |
| 3 |
故k的取值范围为(-
| 1 |
| 3 |
点评:本题考查了函数的奇偶性,以及指数函数的性质,以及导数和函数的最值的关系,培养了学生的转化能力,运算能力,属于中档题

练习册系列答案
相关题目
下列集合中,不同于另外三个集合的是( )
| A、{3} |
| B、M={y∈R|(y-3)2=0} |
| C、M={x=3} |
| D、M={x|x-3=0} |
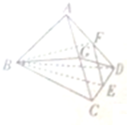
如图,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别是CD、DA、AC的中点,则( )

| A、平面BEF⊥平面BGD |
| B、平面ABC⊥平面ACD |
| C、CD⊥平面BEF |
| D、AB⊥平面BGD |
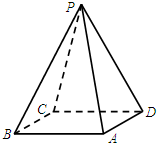 点P为正方形ABCD所在平面外一点,AD=3,PD=2
点P为正方形ABCD所在平面外一点,AD=3,PD=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |