题目内容
袋中共有六个小球其中标记有A,B的红球各一个,标记有a,b,c,d的白球各一个,从中任意选取两个球,
(1)记{A,a}(不考虑顺序)为有一种选取结果写出所有选取结果,并指出所有结果的个数,
(2)求所选的两个球中至少有一个红球的概率.
(1)记{A,a}(不考虑顺序)为有一种选取结果写出所有选取结果,并指出所有结果的个数,
(2)求所选的两个球中至少有一个红球的概率.
考点:列举法计算基本事件数及事件发生的概率,古典概型及其概率计算公式
专题:概率与统计
分析:(1)一一列举出所有的基本事件,得到共有12个,
(2)所选的两个球中至少有一个红球的基本事件是9个,根据概率公式计算即可
(2)所选的两个球中至少有一个红球的基本事件是9个,根据概率公式计算即可
解答:
解:(1)所有的结果共12个,{A,B},{A,a},{A,b},{A,c},{A,d},{B,a},{B,b},{B,c},{B,d},{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},
(2)所选的两个球中至少有一个红球有{A,B},{A,a},{A,b},{A,c},{A,d},{B,a},{B,b},{B,c},{B,d},共9个,
故所选的两个球中至少有一个红球的概率P=
=
(2)所选的两个球中至少有一个红球有{A,B},{A,a},{A,b},{A,c},{A,d},{B,a},{B,b},{B,c},{B,d},共9个,
故所选的两个球中至少有一个红球的概率P=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查了古典概型的概率的计算,关键是一一列举出所有的基本事件,属于基础题

练习册系列答案
相关题目
在△ABC中,三个内角A,B,C的对边分别为a,b,c,若
=
,则∠B的值为( )
| a |
| sinA |
| b |
| cosB |
| A、30° | B、45° |
| C、60° | D、90° |
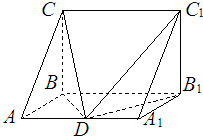 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=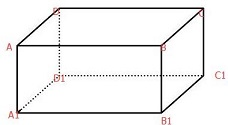 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=3