题目内容
在平面直角坐标系xOy中,已知圆x2+y2-12x+32=0的圆心为Q,过点P(0,2)且斜率为k的直线与圆Q相交于不同的两点A,B
(1)求k的取值范围;
(2)已知|PA|<|PB|,求当k等于何值时,使得|PB|取得最大值.
(1)求k的取值范围;
(2)已知|PA|<|PB|,求当k等于何值时,使得|PB|取得最大值.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)先把圆的方程整理成标准方程,进而求得圆心,设出直线方程代入圆方程整理后,根据判别式大于0求得k 的范围,
(2)由图象可知当直线经过圆心Q,与圆相交时,PB的长度最大,即可求出k的值.
(2)由图象可知当直线经过圆心Q,与圆相交时,PB的长度最大,即可求出k的值.
解答:
解:(1)圆的方程可写成(x-6)2+y2=4,所以圆心为Q(6,0),过P(0,2)
且斜率为k的直线方程为y=kx+2.
代入圆方程得x2+(kx+2)2-12x+32=0,
整理得(1+k2)x2+4(k-3)x+36=0. ①
直线与圆交于两个不同的点A,B等价于△=[4(k-3)2]-4×36(1+k2)=42(-8k2-6k)>0,
解得-
<k<0,即k的取值范围为(-
,0).
(2)由图象可知当直线经过圆心Q,与圆相交时,PB的长度最大,
此时直线y=kx+2过Q(6,0),
则6k+2=0,解得k=-
.
且斜率为k的直线方程为y=kx+2.
代入圆方程得x2+(kx+2)2-12x+32=0,
整理得(1+k2)x2+4(k-3)x+36=0. ①

直线与圆交于两个不同的点A,B等价于△=[4(k-3)2]-4×36(1+k2)=42(-8k2-6k)>0,
解得-
| 3 |
| 4 |
| 3 |
| 4 |
(2)由图象可知当直线经过圆心Q,与圆相交时,PB的长度最大,
此时直线y=kx+2过Q(6,0),
则6k+2=0,解得k=-
| 1 |
| 3 |
点评:本题主要考查直线和圆的 位置关系的应用,利用数形结合是解决本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
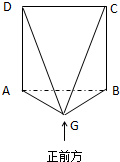 如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.
如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.