题目内容
化简下列式子:C
C
+C
C
+C
C
+…+C
C
= .(1≤k<m≤n,k,m,n∈N).
0 m |
k n |
1 m |
k-1 n |
2 m |
k-2 n |
k m |
0 n |
考点:排列、组合及简单计数问题
专题:排列组合
分析:观察表达式,利用表达式的几何意义,直接根据排列组合公式,易得答案.
解答:
解:在C
C
+C
C
+C
C
+…+C
C
中,
从第一项到最后一项表示从从装有m+n个球(其中m个白球,n个黑球)的口袋中取出k个球所有情况取法总数的和
,
故答案为:
.
0 m |
k n |
1 m |
k-1 n |
2 m |
k-2 n |
k m |
0 n |
从第一项到最后一项表示从从装有m+n个球(其中m个白球,n个黑球)的口袋中取出k个球所有情况取法总数的和
| C | k m+n |
故答案为:
| C | k m+n |
点评:这个题结合考查了推理和排列组合,处理本题的关键是熟练掌握排列组合公式,明白每一项所表示的含义,再结合已知条件进行分析,最后给出正确的答案.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
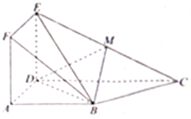 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=