题目内容

等比数列{an]的前n项和为Sn，若S3=2，S6=6，则a10+a11+a12=
 
．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由等比数列的性质知S3，S6-S3，S9-S6，S12-S9构成一个等比数列，可得结论．
解答： 解：由题意若S3=2，S6-S3=4，a10+a11+a12=S12-S9，
由等比数列的性质知S3，S6-S3，S9-S6，S12-S9构成一个等比数列，
∴S12-S9=2•23=16．
故答案为：16
点评：本题考查等比数列的性质，Sk，S2k-Sk，S3k-S2k，…构成一个公比为qk的等比数列，利用这个性质，极大的简化了运算，本题若利用等比数列的前n项和建立方程组求首项与公比，再求和，运算较繁，学习中注意体会性质的运用．
练习册系列答案
相关题目
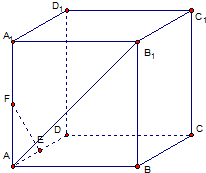如图，在正方体ABCD-A1B1C1D1中，E、F分别是AD，AA1的中点
（1）求直线AB1和直线CC1所成的角的大小
（2）求直线AB1和直线EF所成的角的大小．
化简下列式子：C
 
0
m
C
 
k
n
+C
 
1
m
C
 
k-1
n
+C
 
2
m
C
 
k-2
n
+…+C
 
k
m
C
 
0
n
=
 
．（1≤k＜m≤n，k，m，n∈N）．
设函数f（x）=
x2+bx+c (x≤0)
2 (x＞0)
，若f（-2）=f（0），f（-1）=-3，则关于x的方程f（x）=x的解的个数为
 
．
已知函数f（x）=
2x ，x≤1
log
1
2
x ，x＞1
，则f（f（2））等于
 
．
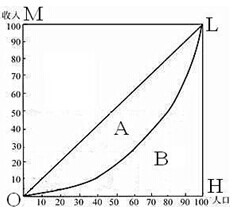基尼系数是衡量一个国家贫富差距的标准．图中横轴OH表示人口（按收入由低到高分组）的累积百分比，纵轴OM表示收入的累积百分比，弧线OL（洛伦兹曲线）与对角线之间的面积A叫做“不平等面积”，折线段OHL与对角线之间的面积（A+B）叫做“完全不平等面积”，不平等面积与完全不平等面积之比等于基尼系数，则：
（1）当洛伦兹曲线为对角线时，社会达到“共同富裕”这是社会主义国家的目标，则此时的基尼系数等于
 

（2）为了估计目前我国的基尼系数，统计得到洛伦兹曲线后，采用随机模拟方法：随机产生两个数组成点（a，b）（其中a，b∈[0，100]）共1000个，其中恰好有300个点恰好落在B区域中，则据此估计该基尼系数为：
 
．
设全集U=R，集合A={x|2＜x≤4}，B={3，4}，则A∩（∁UB）=
 
．
双曲线5x2+ky2=5的一个焦点是（2，0），则k=
 
．
从1，3，5中选2个不同数字，从2，4，6，8中选3个不同数字排成一个五位数，则这些五位数中偶数的个数为（　　）
A、5040B、1440
C、864D、720

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网