题目内容
6.函数y=x+sin|x|,x∈[-π,π]的大致图象是( )| A. |  | B. | 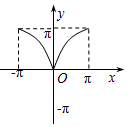 | C. | 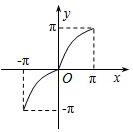 | D. | 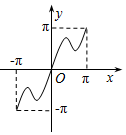 |
分析 根据函数的单调性和函数的变化趋势判断即可.
解答 解:由函数y=x+sin|x|,x∈[-π,π],
可得y=$\left\{\begin{array}{l}{x+sinx,x∈[0,π]}\\{x-sinx,x∈[-π,0)}\end{array}\right.$,
显然函数y在[0,π]上单调递增,且经过点(0,0)、(π,π);
函数y在[-π,0)上也单调递增,且经过点(0,0)、(-π,-π);
且函数y既不是奇函数也不是偶函数,
故选:C
点评 本题考查了函数图象的识别,关键是掌握函数的单调性和函数的变化趋势,属于中档题.

练习册系列答案
相关题目
16.设$f(x)=\frac{x}{{\sqrt{1+{x^2}}}}$,数列{an}满足a1=f(1),an+1=f(an)(n∈N*),则a2017=( )
| A. | $\frac{1}{{\sqrt{2016}}}$ | B. | $\frac{1}{{\sqrt{2017}}}$ | C. | $\frac{1}{{\sqrt{2018}}}$ | D. | $\frac{1}{{\sqrt{2019}}}$ |
17.已知全集U=R,集合A={x|2x<1},B={x|x-2<0},则(∁UA)∩B=( )
| A. | {x|x>2} | B. | {x|0≤x<2} | C. | {x|0<x≤2} | D. | {x|x≤2} |
14.已知平面向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
16.已知某四棱锥的三视图如右图所示,则该几何体的体积为( )
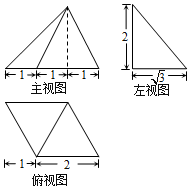

| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 2 | D. | $\frac{{5\sqrt{3}}}{3}$ |
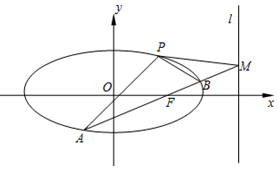 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.
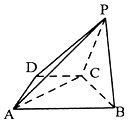 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.