题目内容
10.在平行四边形ABCD中,已知AB=2,AD=l,∠BAD=60°,若E,F分别是BC,CD的中点,则$\overrightarrow{BF}•\overrightarrow{DE}$=( )| A. | 2 | B. | -2 | C. | $\frac{5}{4}$ | D. | $-\frac{5}{4}$ |
分析 可先画出图形,根据条件可得出$\overrightarrow{BF}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB},\overrightarrow{DE}=\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$,带入$\overrightarrow{BF}•\overrightarrow{DE}$进行数量积的运算即可求出该数量积的值.
解答  解:如图,
解:如图,
$\overrightarrow{BF}=\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{DE}=\overrightarrow{DC}+\frac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$;
且AB=2,AD=1,∠BAD=60°;
∴$\overrightarrow{BF}•\overrightarrow{DE}=(\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB})•(\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD})$
=$-\frac{1}{2}{\overrightarrow{AB}}^{2}-\frac{1}{2}{\overrightarrow{AD}}^{2}+\frac{5}{4}\overrightarrow{AD}•\overrightarrow{AB}$
=$-2-\frac{1}{2}+\frac{5}{4}×1×2×\frac{1}{2}$
=$-\frac{5}{4}$.
故选D.
点评 考查向量加法和数乘的几何意义,相等向量和相反向量的概念,以及向量数量积的运算及计算公式.

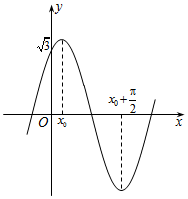 已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )
已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2sin(2x+\frac{π}{3})$ | C. | $f(x)=2sin(x+\frac{π}{6})$ | D. | $f(x)=2sin(x+\frac{π}{3})$ |
| A. |  | B. |  | C. | 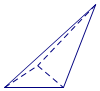 | D. | 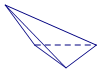 |
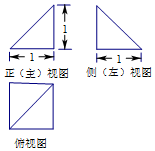
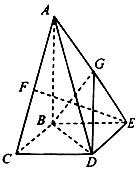 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE=$\sqrt{2}$.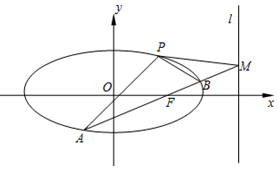 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.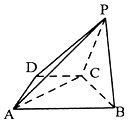 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.