题目内容
19.若kx2-kx+4≥0对一切实数都成立,求k的取值范围.分析 不等式kx2-kx+4≥0对一切实数x都成立,对k讨论,分k=0,k≠0,再由y=kx2-kx+4的图象可得,k>0,且△≤0,由此能够求出k的取值范围.
解答 解:∵不等式kx2-kx+4≥0对一切实数x都成立,
当k=0时,4>0恒成立;
当k≠0,
根据y=kx2-kx+4的图象,可得k>0,且△≤0,
即有k2-16k≤0,
解得0<k≤16.
综上可得,k的取值范围是[0,16].
点评 本题考查二次函数的图象和性质,解题时要抓住二次函数与x轴无交点的特点进行求解.主要考查了二次函数的恒成立问题.二次函数的恒成立问题分两类,一是大于0恒成立须满足开口向上,且判别式小于0,二是小于0恒成立须满足开口向下,且判别式小于0.

练习册系列答案
相关题目
7.如某校高中三年级的300名学生已经编号为0,1,…,299,为了了解学生的学习情况,要抽取一个样本数为60的样本,用系统抽样的方法进行抽取,若第60段所抽到的编号为298,则第1段抽到的编号为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.四棱柱成为平行六面体的充分不必要条件是( )
| A. | 侧面是平行四边形 | B. | 底面是矩形 | ||
| C. | 一个侧面是矩形 | D. | 两相邻侧面均为矩形 |
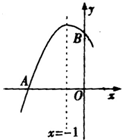 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论: