题目内容
8.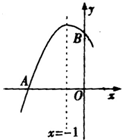 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:①b2>4ac;②2a-b=0;③a-b+c>0;④c<0,
其中正确结论的个数是3.
分析 由抛物线与x轴有两个交点判断①;由对称轴方程判断②;利用f(-1)>0判断③;由f(0)>0判断④.
解答 解:∵图象与x轴有交点,对称轴为x=-$\frac{b}{2a}$=-1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2-4ac>0,
即b2>4ac,①正确;
∵对称轴为x=-$\frac{b}{2a}$=-1,
∴2a=b,
∴2a-b=0,②正确;
由f(-1)>0,得a-b+c>0,③正确;
由f(0)>0,得c>0,④错误.
∴正确结论的个数是3个.
故答案为:3.
点评 本题考查二次函数y=ax2+bx+c的图象和性质,考查二次函数的开口方向、对称轴方程、及函数的零点等问题,是基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
3.某校天文兴趣小组共有学生100人,其中一年级40人,二、三年级各30人,现要利用随机抽样的方法抽取10人参加某项调查,考虑选用简单随机抽样、系统抽样和分层抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为00,01,02,…,99;使用系统抽样时,将学生统一随机编号00,01,02,…,99,
并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①05,10,17,36,47,53,65,76,90,95; ②05,15,25,35,45,55,65,75,85,95;
③08,17,42,48,52,56,61,64,74,88; ④08,15,22,29,48,55,62,78,85,92.
关于上述随机样本的下列结论中,正确的是( )
并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①05,10,17,36,47,53,65,76,90,95; ②05,15,25,35,45,55,65,75,85,95;
③08,17,42,48,52,56,61,64,74,88; ④08,15,22,29,48,55,62,78,85,92.
关于上述随机样本的下列结论中,正确的是( )
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、③都可能为分层抽样 | D. | ①、④都可能为分层抽样 |
18.若对?x,y∈(0,+∞),不等式4xlna<ex+y-2+ex-y-2+2恒成立,则正实数a的最大值是( )
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$e | C. | e | D. | 2e |