题目内容
已知函数f(x)=
且f(-1)=2.
(1)求a的值;
(2)写出f(x)的单调区间;
(3)若函数g(x)=f(x)-m有三个互不相等的零点x1,x2,x3,
①求m的取值范围;
②求x1+x2+x3的取值范围.
|
(1)求a的值;
(2)写出f(x)的单调区间;
(3)若函数g(x)=f(x)-m有三个互不相等的零点x1,x2,x3,
①求m的取值范围;
②求x1+x2+x3的取值范围.
考点:分段函数的应用,函数零点的判定定理
专题:函数的性质及应用
分析:(1)根据分段函数的表达式即可求a的值;
(2)根据分段函数的表达式即可写出f(x)的单调区间;
(3)作出函数f(x)的图象,利用数形结合即可得到结论.
(2)根据分段函数的表达式即可写出f(x)的单调区间;
(3)作出函数f(x)的图象,利用数形结合即可得到结论.
解答:
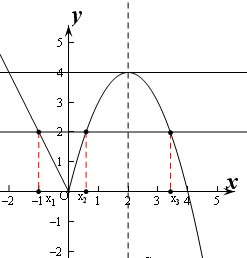 解:(1)∵f(-1)=2,∴f(-1)=-a=2,即a=-2;
解:(1)∵f(-1)=2,∴f(-1)=-a=2,即a=-2;
(2)当a=-2时,f(x)=
,
作出函数f(x)的图象,
则f(x)的单调增区间为(0,2],递减区间为(-∞,0]和[2,+∞).
(3)①若函数g(x)=f(x)-m有三个互不相等的零点x1,x2,x3,
即f(x)=m有三个根,即函数y=f(x)与y=m有三个不同的交点,
则0<m<4,即m的取值范围是(0,4);
②不妨设x1<x2<x3,
则x1<0,x2>0,x3>0,且x2,x3,关于x=2对称,
则x2+x3=2×2=4,
则x1+x2+x3=x1+4<4,
即x1+x2+x3的取值范围是(-∞,4).
 解:(1)∵f(-1)=2,∴f(-1)=-a=2,即a=-2;
解:(1)∵f(-1)=2,∴f(-1)=-a=2,即a=-2;(2)当a=-2时,f(x)=
|
作出函数f(x)的图象,
则f(x)的单调增区间为(0,2],递减区间为(-∞,0]和[2,+∞).
(3)①若函数g(x)=f(x)-m有三个互不相等的零点x1,x2,x3,
即f(x)=m有三个根,即函数y=f(x)与y=m有三个不同的交点,
则0<m<4,即m的取值范围是(0,4);
②不妨设x1<x2<x3,
则x1<0,x2>0,x3>0,且x2,x3,关于x=2对称,
则x2+x3=2×2=4,
则x1+x2+x3=x1+4<4,
即x1+x2+x3的取值范围是(-∞,4).
点评:本题主要考查分段函数的应用,以及函数零点的应用,利用数形结合以及二次函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
 近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4
近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4