题目内容
已知双曲线x2-
=1,那么它的焦点到渐近线的距离为 .
| y2 |
| 3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线的方程求出焦点坐标和一条渐近线方程,由点到直线的距离公式求得焦点到渐近线的距离.
解答:
解:双曲线x2-
=1的焦点F(2,0),一条渐近线的方程为 y=
x,
由点到直线的距离公式可得焦点到渐近线的距离为
=
,
故答案为:
.
| y2 |
| 3 |
| 3 |
由点到直线的距离公式可得焦点到渐近线的距离为
|2
| ||
|
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的标准方程,以及双曲线的简单性质,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
设函数f(x)=log2(x2-4x+a)(a>4),若所有点(s,f(t))(s,t∈[1,3])构成一个正方形区域,则函数f(x)的单调增区间为( )
| A、[1,2] |
| B、[2,3] |
| C、(-∞,2] |
| D、[2,+∞) |
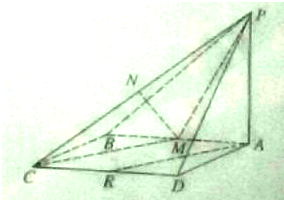 如图,已知矩形ABCD中,PA⊥平面ABCD,M,N,R分别是AB,PC,CD的中点,求证:
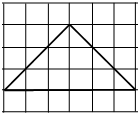
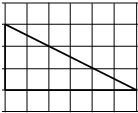
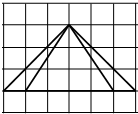
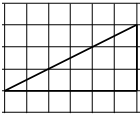
如图,已知矩形ABCD中,PA⊥平面ABCD,M,N,R分别是AB,PC,CD的中点,求证: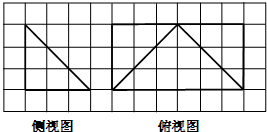 如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )
如图,网格纸的各小格都是正方形,粗实线画出的是一个锥体的侧视图和俯视图,则该锥体的正视图可能是( )