题目内容
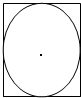
如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
(1)求此几何体的表面积;(2)求此几何体的体积.

(1)求此几何体的表面积;(2)求此几何体的体积.


考点:棱柱、棱锥、棱台的体积,由三视图求面积、体积
专题:空间位置关系与距离
分析:由几何体的三视图知:该几何体是一个侧棱长为2,底面直径为2的圆锥和高为1直径为2的圆柱的组合体,由此能求出此几何体的表面积和体积.
解答:
解:(1)由几何体的三视图知:
该几何体是一个侧棱长为2,底面直径为2的圆锥和高为1直径为2的圆柱的组合体,
∴此几何体的表面积S=2π×1+2π=4π.
(2)此几何体的体积:
V=π×1+
π×
=(
+1)π.
该几何体是一个侧棱长为2,底面直径为2的圆锥和高为1直径为2的圆柱的组合体,
∴此几何体的表面积S=2π×1+2π=4π.
(2)此几何体的体积:
V=π×1+
| 1 |
| 3 |
| 4-1 |
| ||
| 3 |
点评:本题考查几何体的表面积和体积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
若双曲线
-
=1的离心率为2,则其渐近线的斜率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
设x,y满足约束条件
,若目标函数z=
的最大值为2,则z的最小值为( )
|
| y+m |
| x-4 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
各项都是正数的等比数列{an}的公比q≠1,且a2,
a3,a1成等差数列,则
的值为( )
| 1 |
| 2 |
| a3+a4+a5 |
| a4+a5+a6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
某公司招收男职员x名,女职员y名,须满足约束条件
则10x+10y的最大值是( )
|
| A、80 | B、85 | C、90 | D、100 |
