题目内容
已知函数f(x)=1-
-ln(x+1)(a为实常数),若函数f(x)的区间(-1,1)内无极值.则实数a的取值范围为 .
| a |
| x+1 |
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:求导f′(x)=
-
=
,从而可得x=a-1在(-1,1)上没有根,从而解得.
| a |
| (x+1)2 |
| 1 |
| x+1 |
| a-(x+1) |
| (x+1)2 |
解答:
解:∵f(x)=1-
-ln(x+1),
∴f′(x)=
-
=
,
又∵函数f(x)的区间(-1,1)内无极值,
∴a-(x+1)=0在(-1,1)上没有根,
x=a-1在(-1,1)上没有根,
故a-1≤-1或a-1≥1;
故a≤0或a≥2;
故实数a的取值范围为a≤0或a≥2;
故答案为:a≤0或a≥2.
| a |
| x+1 |
∴f′(x)=
| a |
| (x+1)2 |
| 1 |
| x+1 |
| a-(x+1) |
| (x+1)2 |
又∵函数f(x)的区间(-1,1)内无极值,
∴a-(x+1)=0在(-1,1)上没有根,
x=a-1在(-1,1)上没有根,
故a-1≤-1或a-1≥1;
故a≤0或a≥2;
故实数a的取值范围为a≤0或a≥2;
故答案为:a≤0或a≥2.
点评:本题考查了导数的综合应用及恒成立问题,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
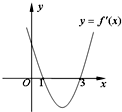 已知函数f(x)=x3+ax2+bx+c的导函数y=f′(x)的图象如图所示,给出下列三个结论:
已知函数f(x)=x3+ax2+bx+c的导函数y=f′(x)的图象如图所示,给出下列三个结论:①f(x)的单调递减区间是(1,3);
②函数f(x)在x=1处取得极小值;
③a=-6,b=9.正确的结论是( )
| A、①③ | B、①② | C、②③ | D、①②③ |
已知
,
为不共共线的非零向量,且|
|=|
|=1,则以下四个向量中模最大者为( )
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
把一个骰子连续抛掷两次,第一次得到的点数为a,第二次得到的点数为b,则事件“a=b”的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|

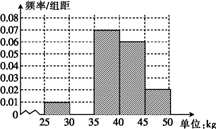 某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).
某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).