题目内容
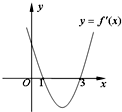已知函数f（x）=x3+ax2+bx+c的导函数y=f′（x）的图象如图所示，给出下列三个结论：①f（x）的单调递减区间是（1，3）；
②函数f（x）在x=1处取得极小值；
③a=-6，b=9．正确的结论是（ ）
| A、①③ | B、①② | C、②③ | D、①②③ |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：通过读图得到函数的单调区间，结合导函数的性质分别对①②③进行判断，从而得到答案．
解答：
解：由题意得：函数f（x）在（-∞，1）递增，在（1，3）递减，在（3，+∞）递增，
∴f（x）在x=1处取到极大值，且
，解得：a=-6，b=9，
∴①③正确，②错误，
故选：A．
∴f（x）在x=1处取到极大值，且
|
∴①③正确，②错误，
故选：A．
点评：本题考查了导数的应用，考查了函数的单调性，函数的极值问题，是一道基础题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
设F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，若在双曲线的右支上存在点P，满足|PF2|=|F1F2|，且原点O到直线PF1的距离等于双曲线的实半轴长，则该双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、4x±3y=0 |
| B、3x±5y=0 |
| C、3x±4y=0 |
| D、5x±3y=0 |