题目内容
13．已知函数$f（x）=1-2{cos^2}（x+\frac{π}{4}）$，下列说法正确的是（ ）| A． | f（x）是最小正周期为π的奇函数 | B． | f（x）是最小正周期为π的偶函数 | ||
| C． | f（x）是最小正周期为$\frac{π}{2}$的偶函数 | D． | f（x）是最小正周期为$\frac{π}{2}$的奇函数 |
分析 利用倍角公式，诱导公式化简可得函数解析式f（x）=sin2x，利用三角函数的周期性及其求法，正弦函数的图象和性质即可得解．
解答 解：∵$f（x）=1-2{cos^2}（x+\frac{π}{4}）$=1-[1+cos（2x+$\frac{π}{2}$）]=sin2x，
∴可得f（x）是最小正周期为π的奇函数．
故选：A．
点评 本题主要考查了倍角公式，诱导公式，三角函数的周期性及其求法，正弦函数的图象和性质的综合应用，考查了数形结合思想和转化思想，属于基础题．
练习册系列答案
优生乐园系列答案
相关题目
3．设p：$（3{x^2}+ln3）'=6x+\frac{1}{3}$，q：函数y=（3-x2）ex的单调递增区是（-3，1），则p与q的复合命题的真假是（ ）
| A． | “p∨q”假 | B． | “p∧q”真 | C． | “￢q”真 | D． | “p∨q”真 |
4．函数$y=\frac{1}{lg（x-1）}$的定义域为（ ）
| A． | （-∞，1） | B． | （1，+∞） | C． | （1，2）∪（2，+∞） | D． | （1，3）∪（3，+∞） |
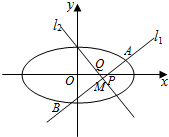已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（0，1），离心率为 $\frac{\sqrt{3}}{2}$，点O为坐标原点．