题目内容
18.已知在等比数列{an}中,前n项和${S_n}={2^n}+t$,则数列的通项公式an=2n-1.分析 由题意写出数列的前3项,解方程可得t值,可得数列的首项和公比,可得通项公式.
解答 解:∵等比数列{an}中,前n项和${S_n}={2^n}+t$,
∴a1=S1=2+t,a2=S2-S1=2,a3=S3-S2=4,
∴22=4(2+t),解得t=-1,
∴a1=2+t=1,公比q=2,
∴an=2n-1
故答案为:2n-1
点评 本题考查等比数列的通项公式,求出数列的首项和公比是解决问题的关键,属基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
9.已知$cos(\frac{π}{4}+θ)=\frac{2}{3}\sqrt{2}$,则sin2θ=( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
13.已知函数$f(x)=1-2{cos^2}(x+\frac{π}{4})$,下列说法正确的是( )
| A. | f(x)是最小正周期为π的奇函数 | B. | f(x)是最小正周期为π的偶函数 | ||
| C. | f(x)是最小正周期为$\frac{π}{2}$的偶函数 | D. | f(x)是最小正周期为$\frac{π}{2}$的奇函数 |
10.已知圆M:(x+$\sqrt{7}$)2+y2=64,定点N($\sqrt{7}$,0),点P为圆M上的动点,点Q在NP上,点G 在线段MP上,且满足$\overrightarrow{NP}$=2$\overrightarrow{NQ}$,$\overrightarrow{GQ}$•$\overrightarrow{NP}$=0,则点G的轨迹方程是( )
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{64}+\frac{y^2}{57}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{57}=1$ |
7.等比数列{an}中,S2=2,S4=8,则S6=( )
| A. | -32 | B. | 32 | C. | -26 | D. | 26 |
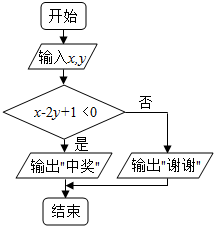 某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.
某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.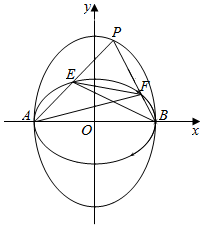 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.