题目内容
8.己知圆C过椭圆$\frac{{x}^{2}}{2}+{y}^{2}$=1的右焦点,且圆心在x的正半轴上,且直线l:y=x-1被圆C截得的弦长为2$\sqrt{2}$.(1)求圆C的标准方程;
(2)从圆C外一点P向圆引一条切线,切点为M,O为原点,且有|PM|=|PO|,求使|PM|最小的P点的坐标.
分析 (1)求得椭圆的右焦点,设圆的方程为(x-a)2+y2=r2,a>0,代入(1,0),运用点到直线的距离公式和圆的弦长公式,计算求得a=3,r=2,即可得到圆的标准方程;
(2)求出圆心C,半径r.设P(x,y).由切线的性质可得:CM⊥PM,利用|PM|=|PO|,可得x=$\frac{5}{6}$,即P在直线x=$\frac{5}{6}$上,再利用垂直时线段最短,即可得到所求点.
解答 解:(1)椭圆$\frac{{x}^{2}}{2}+{y}^{2}$=1的右焦点为(1,0),
设圆的方程为(x-a)2+y2=r2,a>0,
由题意可得(1-a)2=r2,a>0,
又2$\sqrt{2}$=2$\sqrt{{r}^{2}-(\frac{|a-1|}{\sqrt{2}})^{2}}$,
解得a=3,r=2,
可得圆的方程为(x-3)2+y2=4;
(2)如图所示(x-3)2+y2=4的圆心C(3,0),半径r=2.
设P(x,y),
∵CM⊥PM,
∴|PM|=$\sqrt{|PC{|}^{2}-{r}^{2}}$=$\sqrt{(x-3)^{2}+{y}^{2}-4}$.
∵|PM|=|PO|,
∴$\sqrt{(x-3)^{2}+{y}^{2}-4}$=$\sqrt{{x}^{2}+{y}^{2}}$,
化为x=$\frac{5}{6}$,即P在直线x=$\frac{5}{6}$上,
∴|PM|2=x2+y2=$\frac{25}{36}$+y2
当y=0时,|PM|2取得最小值$\frac{25}{36}$,
即|PM|取得最小值$\frac{5}{6}$,此时P($\frac{5}{6}$,0).
点评 本题考查圆的方程的求法,注意运用待定系数法,以及圆的弦长公式的运用,考查圆的切线的性质和勾股定理的运用,考查运算能力,属于中档题.

| A. | 甲、乙恰有一人的试跳成绩没有超过2米 | |
| B. | 甲、乙至少有一人的试跳成绩没有超过2米 | |
| C. | 甲、乙两人的试跳成绩都没有超过2米 | |
| D. | 甲、乙至少有一人的试跳成绩超过2米 |
(1)求n的值和月均用电量的平均数估计值;
(2)如果用分层抽样的方法从用电量小于30度的居民中抽取5位居民,再从这5位居民中选2人,那么至少有1位居民月均用电量在20至30度的概率是多少?
| 分组 | 频数 | 频率 |
| [0,10) | 0.05 | |
| [10,20) | 0.10 | |
| [20,30) | 30 | |
| [30,40) | 0.25 | |
| [40,50) | 0.15 | |
| [50,60] | 15 | |
| 合计 | n | 1 |
| A. | b2 | B. | ab | C. | ac | D. | bc |
| A. | f(x)是最小正周期为π的奇函数 | B. | f(x)是最小正周期为π的偶函数 | ||
| C. | f(x)是最小正周期为$\frac{π}{2}$的偶函数 | D. | f(x)是最小正周期为$\frac{π}{2}$的奇函数 |
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
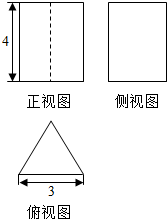
| A. | 36 | B. | 36$+\frac{9\sqrt{3}}{4}$ | C. | 36$+\frac{9\sqrt{3}}{2}$ | D. | 18$+\frac{9\sqrt{3}}{2}$ |
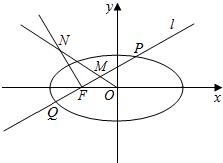 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{2}$),离心率为$\frac{\sqrt{6}}{3}$,点O为坐标原点.