题目内容
等比数列{an}中，a3=-1，a7=-4，则a3和a7的等比中项为 ．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比中项的性质，建立方程即可得到结论．
解答：
解：∵a3=-1，a7=-4，
∴a3和a7的等比中项是a5，
则（a5）2=a3a7=4，
即a5=±2，
∵a5=a3q2=-q2＜0，
∴a5=-2，
故答案为；-2
∴a3和a7的等比中项是a5，
则（a5）2=a3a7=4，
即a5=±2，
∵a5=a3q2=-q2＜0，
∴a5=-2，
故答案为；-2
点评：本题主要考查等比数列的性质，利用等比中项的定义是解决本题的关键，注意等比数列中的符号问题．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，椭圆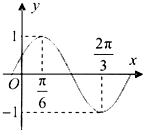
已知函数f（x）=sin（ωx+φ）（ω＞0，φ＜