题目内容
已知函数f(x)=alnx+bx2在点(1,f(1))处的切线方程为x-y-1=0
(Ⅰ)(ⅰ)求f(x)的表达式;
(ⅱ)对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线y=ex在切线y=x+1的上方,故有不等式ex≥x+1.类比上述推理,对于函数f(x),直接写出一个相类似的结论(不需证明).
( II)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数f(x)为g(x)=
-lnx(t∈R)的一个“上界函数”,求t的取值范围;
(Ⅲ)当m>0时,讨论F(x)=f(x)+
-
x在区间(0,2)上极值点的个数.
(Ⅰ)(ⅰ)求f(x)的表达式;
(ⅱ)对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线y=ex在切线y=x+1的上方,故有不等式ex≥x+1.类比上述推理,对于函数f(x),直接写出一个相类似的结论(不需证明).
( II)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数f(x)为g(x)=
| t |
| x |
(Ⅲ)当m>0时,讨论F(x)=f(x)+
| x2 |
| 2 |
| m2+1 |
| m |
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)(ⅰ)利用导数的几何意义,求得函数的切线方程,比较系数即可得出a、b的值,写出函数解析式;
(ⅱ)由题意类比即可写出结论;
(Ⅱ)根据上界函数的定义,可得f(x)≥g(x)恒成立即2lnx-
≥0恒成立,所以 t≤2xlnx恒成立,利用导数求得函数h(x)=2xlnx的最小值,即可得出结论;
(Ⅲ)由极值的定义,对m分类讨论,利用导数即可研究函数的极值.
(ⅱ)由题意类比即可写出结论;
(Ⅱ)根据上界函数的定义,可得f(x)≥g(x)恒成立即2lnx-
| t |
| x |
(Ⅲ)由极值的定义,对m分类讨论,利用导数即可研究函数的极值.
解答:
解:( I)(ⅰ)因为f′(x)=
+2bx,且切点为(1,b),所以切线方程为y=(a+2b)(x-1)+b,
因为切线为y=x-1,所以a=1,b=0,∴f(x)=lnx…(3分)
(ⅱ)对于函数f(x)=lnx,有不等式lnx≤x-1成立.…(6分)
( II)因为f(x)≥g(x)恒成立即2lnx-
≥0恒成立,所以 t≤2xlnx恒成立
令h(x)=2xlnx,∴h′(x)=2lnx+2函数递减区间为(0,
),递增区间为(
,+∞)
所以h(x)min=h(
)=-
,故t≤-
…(10分)
(Ⅲ)F′(x)=
+x-
=
=
当
<m<1或1<m<2时,F(x)在(0,2)上有一个极大值点和一个极小值点…(12分)
当0<m≤
或m≥2时,F(x)在(0,2)上有一个极大值点,无极小值点…(14分)
| a |
| x |
因为切线为y=x-1,所以a=1,b=0,∴f(x)=lnx…(3分)
(ⅱ)对于函数f(x)=lnx,有不等式lnx≤x-1成立.…(6分)
( II)因为f(x)≥g(x)恒成立即2lnx-
| t |
| x |
令h(x)=2xlnx,∴h′(x)=2lnx+2函数递减区间为(0,
| 1 |
| e |
| 1 |
| e |
所以h(x)min=h(
| 1 |
| e |
| 2 |
| e |
| 2 |
| e |
(Ⅲ)F′(x)=
| 1 |
| x |
| m2+1 |
| m |
| mx2-(m2+1)x+m |
| mx |
| (mx-1)(x-m) |
| mx |
当
| 1 |
| 2 |
当0<m≤
| 1 |
| 2 |
点评:本题主要考查导数的几何意义及利用导数研究函数的极值、最值等知识,考查学生的分析问题、解决问题的能力及运算求解能力,考查分类讨论思想及等价转化思想的运用能力,属于难题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
在单位圆上,点P从(0,1)出发,沿单位圆x2+y2=1顺时针方向运动
弧长到达Q点,则Q 点的坐标为( )
| 2π |
| 3 |
A、(-
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(-
|
阅读如图所示的程序框图,运行相应的程序,若输入的值为9,则输出的值为( )


| A、1064 | B、1065 |
| C、1067 | D、1068 |
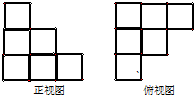
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )

| A、12 | B、13 | C、14 | D、15 |