题目内容
在直角坐标系xOy中,设P是曲线C:xy=1(x>0)上任意一点,l是曲线C在点P处的切线,且l交坐标轴于A,B两点,则下列结论正确的是( )
| A、△OAB的面积为定值2 |
| B、△OAB的面积有最小值为3 |
| C、△OAB的面积有最大值为4 |
| D、△OAB的面积的取值范围是[3,4] |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:设P(a,
),求出曲线C在点P处的切线方程,再计算面积,即可得出结论.
| 1 |
| a |
解答:
解:由题意,y=
(x>0),则y′=-
设P(a,
),则曲线C在点P处的切线方程为y-
=-
(x-a),
x=0可得y=
;y=0可得x=2a,
∴△OAB的面积为
×
×2a=2,即定值2,
故选:A.
| 1 |
| x |
| 1 |
| x2 |
设P(a,
| 1 |
| a |
| 1 |
| a |
| 1 |
| a2 |
x=0可得y=
| 2 |
| a |
∴△OAB的面积为
| 1 |
| 2 |
| 2 |
| a |
故选:A.
点评:本题考查利用导数研究曲线上某点切线方程,考查学生的计算能力,确定切线方程是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知平面向量
=(2cos2x,sin2x),
=(cos2x,-2sin2x),f(x)=
•
,要得到y=sin2x+
cos2x的图象,只需要将y=f(x)的图象( )
| a |
| b |
| a |
| b |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
过边长为2的正方形中心作直线l将正方形分为两个部分,将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为( )
| A、2 | ||
B、2(3-
| ||
C、4(2-
| ||
D、4(3-2
|
在正三棱柱ABC-A1B1C1中,AB=4,点D在棱BB1上,若BD=3,则AD与平面AA1C1C所成角的正切值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
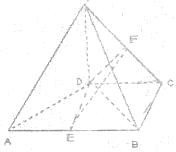 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.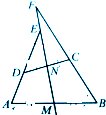 已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证:
已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证: