题目内容
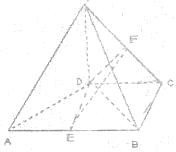 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E,F分别为AB,PC的中点,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求证:PC⊥平面DEF;
(2)求点A到平面PBD的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明:PC⊥DF,DE⊥PC,利用线面垂直的判定定理证明PC⊥平面DEF;
(2)证明AD⊥平面PBD,即可求点A到平面PBD的距离.
(2)证明AD⊥平面PBD,即可求点A到平面PBD的距离.
解答:
(1)证明:∵PD=DC,F为PC的中点,
∴PC⊥DF,
∵四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,∠BCD=90°
∴DE⊥平面PDC,
∴DE⊥PC,
∵DE∩DF=D,
∴PC⊥平面DEF;
(2)解:∵DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
∴AD⊥DB,
∵PD⊥AD,PD∩DB=D,
∴AD⊥平面PBD
∴AD=
为点A到平面PBD的距离.
∴PC⊥DF,
∵四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,∠BCD=90°
∴DE⊥平面PDC,
∴DE⊥PC,
∵DE∩DF=D,
∴PC⊥平面DEF;
(2)解:∵DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
∴AD⊥DB,
∵PD⊥AD,PD∩DB=D,
∴AD⊥平面PBD
∴AD=
| 2 |
点评:本题考查线面垂直的判定,考查点到平面的距离,正确证明线面垂直是关键.

练习册系列答案
相关题目
在直角坐标系xOy中,设P是曲线C:xy=1(x>0)上任意一点,l是曲线C在点P处的切线,且l交坐标轴于A,B两点,则下列结论正确的是( )
| A、△OAB的面积为定值2 |
| B、△OAB的面积有最小值为3 |
| C、△OAB的面积有最大值为4 |
| D、△OAB的面积的取值范围是[3,4] |
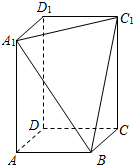 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.