题目内容
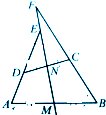已知：如图，M，N是四边形ABCD中AB和CD的中点，AD的延长线、BC的延长线分别交直线MN与点E，F，求证：| ED |
| FC |
| EA |
| FB |
考点：相似三角形的性质
专题：证明题,推理和证明
分析：分别过C，D两点作AB的平行线，交MN或MN的延长线于G，H，证明
=
，即可得出结论．
| FC |
| FB |
| ED |
| EA |
解答：
证明：分别过C，D两点作AB的平行线，交MN或MN的延长线于G，H
∵CG‖AB，∴
=
，
∵DH‖AB，∴
=
，
∵CG‖AB，DH‖AB，
∴CG‖DH，又N是CD的中点，∠DNH=∠CNG，
∴△DNH≌△CNG
∴CG=DH
又M是AB的中点，MB=MA
∴
=
，
∴
=
．
证明：分别过C，D两点作AB的平行线，交MN或MN的延长线于G，H ∵CG‖AB，∴
| FC |
| FB |
| CG |
| MB |
∵DH‖AB，∴
| ED |
| EA |
| DH |
| MA |
∵CG‖AB，DH‖AB，
∴CG‖DH，又N是CD的中点，∠DNH=∠CNG，
∴△DNH≌△CNG
∴CG=DH
又M是AB的中点，MB=MA
∴
| FC |
| FB |
| ED |
| EA |
∴
| ED |
| FC |
| EA |
| FB |
点评：本题考查平行线的性质，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
在直角坐标系xOy中，设P是曲线C：xy=1（x＞0）上任意一点，l是曲线C在点P处的切线，且l交坐标轴于A，B两点，则下列结论正确的是（ ）
| A、△OAB的面积为定值2 |
| B、△OAB的面积有最小值为3 |
| C、△OAB的面积有最大值为4 |
| D、△OAB的面积的取值范围是[3，4] |
若执行如图所示的程序框图，则输出的结果s=（ ）
| A、8 | B、9 | C、10 | D、11 |