题目内容
17.数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N*,则an=n2.分析 化简可得$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n}$+1,从而证明{$\frac{{a}_{n}}{n}$}是以1为首项,1为公差的等差数列,从而求得.
解答 解:∵nan+1=(n+1)an+n(n+1),
∴$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n}$+1,
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,
又∵$\frac{{a}_{1}}{1}$=1,
∴{$\frac{{a}_{n}}{n}$}是以1为首项,1为公差的等差数列,
∴$\frac{{a}_{n}}{n}$=1+(n-1)1=n,
故an=n2,
故答案为:n2.
点评 本题考查了等差数列的判断与应用,同时考查了构造法的应用,属于中档题.

练习册系列答案
相关题目
12.设全集U=R,已知集合A={-2,-1,0,1,2,3},B={x|$\frac{3}{x-1}$+1≥0},则集合A∩∁UB=( )
| A. | {-1,0,1} | B. | {-1,0} | C. | {-2,-1,0,1} | D. | {-1,0,1,2} |
2.设命题p:函数y=-xsinx的图象关于原点对称,
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
9.某火锅店为了了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:
(Ⅰ)求y关于x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(Ⅱ)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
(Ⅱ)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额
附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
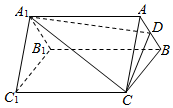 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.