题目内容
8．若P=|x|x2-2x-3＜0}，Q={x|x＞a}，且P∩Q=P，则实数a的取值范围是（-∞，-1]．分析 集合P为一个二次不等式的解集，先解出P=（-1，3），而Q=（a，+∞），再由P∩Q=P，P⊆Q，利用数轴可以求出实数a的取值范围．
解答 解：集合P=|x|x2-2x-3＜0}，化简得P=（-1，3），
而Q={x|x＞a}=（a，+∞），
∵P∩Q=P，∴P⊆Q，
∴a≤-1．
故答案为：（-∞，-1]．
点评 本题考查集合的关系、解二次不等式及数形结合思想，属基本运算的考查．解题时应该注意，在区间端点等号是否成立，对题意的影响．
练习册系列答案
相关题目
18．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的右焦点F作一条渐近线的垂线，垂足为P，线段OP的垂直平分线交y轴于点Q（其中O为坐标原点）．若△OFP的面积是△OPQ的面积的4倍，则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
19．
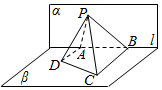如图，已知平面α∩平面β=l，α⊥β．A、B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，DA=4，AB=6，CB=8．P是平面α上的一动点，且有∠APD=∠BPC，则四棱锥P-ABCD体积的最大值是（ ）
如图，已知平面α∩平面β=l，α⊥β．A、B是直线l上的两点，C、D是平面β内的两点，且DA⊥l，CB⊥l，DA=4，AB=6，CB=8．P是平面α上的一动点，且有∠APD=∠BPC，则四棱锥P-ABCD体积的最大值是（ ）| A． | 48 | B． | 16 | C． | $24\sqrt{3}$ | D． | 144 |
如图，梯形ABEF中，AF∥BE，AB⊥AF，且AB=BC=AD=DF=2CE=2，沿DC将梯形CDFE折起，使得平面CDFE⊥平面ABCD．
20．设集合A={x|$\frac{\sqrt{2}}{2}$≤2x≤$\sqrt{2}}\right\}$，B={x|lnx＜0}，则A∩B=（ ）
| A． | （-$\frac{1}{2}$，$\frac{1}{2}$） | B． | （0，$\frac{1}{2}$） | C． | [$\frac{1}{2}$，1） | D． | （0，$\frac{1}{2}$] |