题目内容
2.设命题p:函数y=-xsinx的图象关于原点对称,命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
分析 由于函数y=-xsinx是偶函数,在区间[0,$\frac{π}{2}$]上单调递减即可得出.
解答 解:命题p:函数y=-xsinx是偶函数,其图象关于y轴对称,因此p是假命题.
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,是真命题.
∴只有¬p∧q是真命题.
故选:B.
点评 本题考查了函数的单调性奇偶性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2,m),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
14.若数列$\sqrt{2}$,$\sqrt{5}$,$2\sqrt{2}$,$\sqrt{11}$,$\sqrt{14}$,…,则$4\sqrt{2}$是这个数列的第( )项.
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
11.随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如表所示:
(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\hat y=\hat bx+\hat a$,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年份(x) | 2012 | 2013 | 2014 | 2015 | 2016 |
| 家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程$\hat y=\hat bx+\hat a$,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
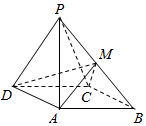 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.