题目内容
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED,点Q满足
=λ
(λ>0).
(1)求证:BD⊥平面POA;
(2)求PB的最小值,并探究此时直线OQ与平面PBD所成的角是否一定大于
?
| AQ |
| QP |

(1)求证:BD⊥平面POA;
(2)求PB的最小值,并探究此时直线OQ与平面PBD所成的角是否一定大于
| π |
| 4 |
考点:直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)因为折叠之后,AO与OC仍然垂直于EF,而BD与AC平行,则BD也与AO、OC垂直,则可证BD与平面POA垂直;
(2)先根据题意建立空间直角坐标系,将几何问题转化为空间向量的计算问题,先给出相关的点(已知与所求)的坐标,求出向量PB的坐标,根据模长公式把PB表示成PO长度x的函数,从而把问题最终转化为函数的最值问题.
(2)先根据题意建立空间直角坐标系,将几何问题转化为空间向量的计算问题,先给出相关的点(已知与所求)的坐标,求出向量PB的坐标,根据模长公式把PB表示成PO长度x的函数,从而把问题最终转化为函数的最值问题.
解答:
(1)证明:∵菱形ABC的对角线互相垂直,∴BD⊥A,∴BD⊥A,
∵EF⊥A,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFE=EF,且PO?平面PEF,
∴PO⊥平面ABFED,∵BD?平面ABFED,∴PO⊥BD
∵AO∩PO=O,∴BD⊥平面POA.
(2)如图,以O为原点,建立空间直角坐标系O-xyz.
设AO∩BD=H,因为∠DAB=60°,所以△BDC为等边三角形,
故BD=4,HB=2,HC=2
.又设PO=x,则OH=2
-x,OA=4
-x.
所以O(0,0,0),P(0,0,x),B(2
-x,2,0),故
=
-
=(2
-x,2,-x),
所以|
|=
=
当x=
时,|
min=
|.此时PO=
,OH=
,
设平面PBD的法向量为
=(x,y,z),则
•
=0,
•
=0.
∵
=(
,2,-
),
=(0,-4,0),∴
,
取x=1,解得:y=0,z=1,所以
=(1,0,1).
设点Q的坐标为(a,0,c),OP=
,则A(3
,0,0),B(
,2,0),D(
,-2,0),P(0,0,
).
所以
=(a-3
,0,c),
=(-a,0,
-c),
∵
=λ
,

∴
⇒
.
∴Q(
,0,
),
∴
=(
,0,
),
设直线OQ与平面PBD所成的角θ,
∴sinθ=|cos<
,
>|=
=
=
=
=
,
又∵λ>0∴sinθ>
,∵θ∈[0,
],∴θ>
.
因此直线OQ与平面PBD所成的角大于
,即结论成立.
∵EF⊥A,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFE=EF,且PO?平面PEF,
∴PO⊥平面ABFED,∵BD?平面ABFED,∴PO⊥BD
∵AO∩PO=O,∴BD⊥平面POA.
(2)如图,以O为原点,建立空间直角坐标系O-xyz.
设AO∩BD=H,因为∠DAB=60°,所以△BDC为等边三角形,
故BD=4,HB=2,HC=2
| 3 |
| 3 |
| 3 |
所以O(0,0,0),P(0,0,x),B(2
| 3 |
| PB |
| OB |
| OP |
| 3 |
所以|
| PB |
(2
|
2(x-
|
当x=
| 3 |
| PB |
| 10 |
| 3 |
| 3 |
设平面PBD的法向量为
| n |
| n |
| PB |
| n |
| BD |
∵
| PB |
| 3 |
| 3 |
| BD |
|
取x=1,解得:y=0,z=1,所以
| n |
设点Q的坐标为(a,0,c),OP=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
所以
| AQ |
| 3 |
| QP |
| 3 |
∵
| AQ |
| QP |

∴
|
|
∴Q(
3
| ||
| λ+1 |
| ||
| λ+1 |
∴
| OQ |
3
| ||
| λ+1 |
| ||
| λ+1 |
设直线OQ与平面PBD所成的角θ,
∴sinθ=|cos<
| OQ |
| n |
|
| ||||
|
|
|
| ||||||||||||
|
| |3+λ| | ||||
|
=
| 1 | ||
|
|
| 1 | ||
|
1+
|
又∵λ>0∴sinθ>
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |
因此直线OQ与平面PBD所成的角大于
| π |
| 4 |
点评:利用向量法求线面角的方法①分别求出斜线和它在平面内的射影直线的方向向量,转化为两个方向向量间的夹角;②求出斜线的方向向量与平面的法向量,则这两个向量间所夹得的锐角或钝角的补角,取其余角即为所求.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1的棱长为a,M为AC1的中点,N为BB1的中点,则|MN|为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2a |
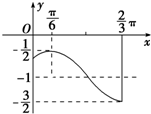 如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.
如图,是函数y=Asin(ωx+φ)+k(A>0,ω>0)的一段图象.