题目内容
已知点P（2，-1）．
（1）求过点P且与原点距离为2的直线l的方程；
（2）求过点P且与原点距离最大的直线l的方程，最大距离是多少？
（1）求过点P且与原点距离为2的直线l的方程；
（2）求过点P且与原点距离最大的直线l的方程，最大距离是多少？
考点：点到直线的距离公式
专题：直线与圆
分析：（1）对直线l的斜率k不存在与存在时分类讨论，再利用点到直线的距离公式及其点斜式即可得出；
（2）即与OP垂直的直线为距离最大的．再利用相互垂直的直线斜率之间的关系即可得出．
（2）即与OP垂直的直线为距离最大的．再利用相互垂直的直线斜率之间的关系即可得出．
解答：
解：（1）①当l的斜率k不存在时显然成立，此时l的方程为x=2．
②当l的斜率k存在时，
设l：y+1=k（x-2），即kx-y-2k-1=0，
由点到直线的距离公式得，
=2，解得k=
，
∴l：3x-4y-10=0．
故所求l的方程为x=2或3x-4y-10=0．
（2）即与OP垂直的直线为距离最大的．
∵kOP=-
，
∴kl=2．
∴直线为2x-y-5=0．
最大距离d=
=
．
②当l的斜率k存在时，
设l：y+1=k（x-2），即kx-y-2k-1=0，
由点到直线的距离公式得，
| |-2k-1| | ||
|
| 3 |
| 4 |
∴l：3x-4y-10=0．
故所求l的方程为x=2或3x-4y-10=0．
（2）即与OP垂直的直线为距离最大的．
∵kOP=-
| 1 |
| 2 |
∴kl=2．
∴直线为2x-y-5=0．
最大距离d=
| (-2)2+12 |
| 5 |
点评：本题考查了点到直线的距离公式、点斜式、相互垂直的直线斜率之间的关系、分类讨论思想方法等基础知识与基本技能方法，属于中档题．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
将自然数的前5个数：（1）排成1，2，3，4，5；（2）排成5，4，3，2，1；（3）排成2，1，5，3，4；（4）排成4，1，5，3，2．那么，可以叫做数列的只有（ ）
| A、（1） |
| B、（1），（2） |
| C、（1），（2），（3） |
| D、（1），（2），（3），（4） |
如图，直线a在α内，b在β内，α⊥β，α∩β=c，∠1=∠2=60°则a、b所成角θ的余弦值为（ ）
| A、1 | ||
B、-
| ||
C、
| ||
D、
|
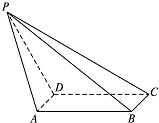如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2
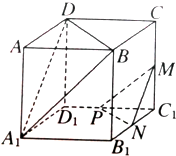在如图所示的正方体ABCD-A1B1C1D1中．