题目内容
已知函数f(x)=cos4x-2sinxcosx-sin4x
(1)化简 f(x)并求f(x)的振幅、相位、初相;
(2)当x∈[0,2π]时,求f(x)的最小值以及取得最小值时x的集合.
(1)化简 f(x)并求f(x)的振幅、相位、初相;
(2)当x∈[0,2π]时,求f(x)的最小值以及取得最小值时x的集合.
考点:y=Asin(ωx+φ)中参数的物理意义,两角和与差的正弦函数,二倍角的余弦,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(1)由题意三角函数公式化简可得f(x)=
sin(2x+
),由参数的意义可得;
(2)令2x+
=-
+2kπ,可得函数取最小值时的x值.
| 2 |
| 3π |
| 4 |
(2)令2x+
| 3π |
| 4 |
| π |
| 2 |
解答:
解:(1)由题意可得f(x)=cos4x-2sinxcosx-sin4x
=(cos2x-sin2x)(cos2x+sin2x)-2sinxcosx
=cos2x-sin2x=
sin(2x+
)
∴振幅是
;相位为:2x+
;初相为:
(2)令2x+
=-
+2kπ,
解得x=-
+kπ,k∈Z,
∵x∈[0,2π],
∴当取k=1,2时,x=
,
∴f(x)取得最小值-
取最小值时x的集合为{
,
}.
=(cos2x-sin2x)(cos2x+sin2x)-2sinxcosx
=cos2x-sin2x=
| 2 |
| 3π |
| 4 |
∴振幅是
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
(2)令2x+
| 3π |
| 4 |
| π |
| 2 |
解得x=-
| 5π |
| 8 |
∵x∈[0,2π],
∴当取k=1,2时,x=
| 3π |
| 8 |
| 11π |
| 8 |
∴f(x)取得最小值-
| 2 |
取最小值时x的集合为{
| 3π |
| 8 |
| 11π |
| 8 |
点评:本题考查三角函数参数的意义,属基础题.

练习册系列答案
相关题目
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则φ=( )

| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|

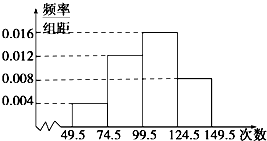 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知如图:第一小组的频数为5.