题目内容
若|
|=|
|=|
|=1,且<
,
>=
,则(
+
-
)•(
+
+
)=( )
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
| a |
| b |
| 2 |
| c |
| a |
| b |
| 2 |
| c |
| A、0 | B、1 | C、2 | D、3 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:运用向量垂直的条件:数量积为0,以及向量的平方即为模的平方,计算即可得到所求.
解答:
解:若|
|=|
|=|
|=1,且<
,
>=
,
则
•
=0,
则(
+
-
)•(
+
+
)=(
+
)2-2
2
=
2+
2+2
•
-2
2=1+1-2=0,
故选A.
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
则
| a |
| b |
则(
| a |
| b |
| 2 |
| c |
| a |
| b |
| 2 |
| c |
| a |
| b |
| c |
=
| a |
| b |
| a |
| b |
| c |
故选A.
点评:本题考查向量的数量积的性质,向量垂直的条件:数量积为0,向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知一个几何体的三视图如图所示,根据图中尺寸可得该几何体的体积为( )

| A、36π | B、24π |
| C、15π | D、12π |
已知|
+
|=
,|
-
|=
,|
|=2,则|
|=( )
| a |
| b |
| 19 |
| a |
| b |
| 7 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
平行四边形ABCD中,∠CBA=120°,AD=4,对角线BD=2
,将其沿对角线BD折起,使平面ABD⊥平面BCD,若四面体ABCD顶点在同一个球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、32
| ||||
| D、2π |
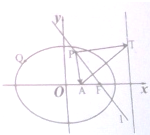 如图,Q为椭圆E:
如图,Q为椭圆E: