题目内容
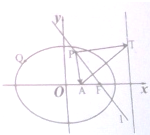 如图,Q为椭圆E:
如图,Q为椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| PT |
(1)AP长是否为定值?若是,求出该定值,若不是,说明理由.
(2)求PQ最小值.
考点:平面向量数量积的运算
专题:向量与圆锥曲线
分析:(1)由题意设P(x,y),T(4,y1),由数量积的运算和垂直的条件列出方程,化简后得到关于x、y的方程,判断出点P的轨迹,即可得|AP|的长是定值;
(2)由题意求出a,b得椭圆的标准方程,设Q(x0,y0)(-3≤x0≤3),由点在椭圆上得坐标椭圆的方程,由|PQ|=|CP|-|CQ|列出式子,利用二次函数的性质可求得|PQ|最小值.
(2)由题意求出a,b得椭圆的标准方程,设Q(x0,y0)(-3≤x0≤3),由点在椭圆上得坐标椭圆的方程,由|PQ|=|CP|-|CQ|列出式子,利用二次函数的性质可求得|PQ|最小值.
解答:
解:(1)由题意设P(x,y),T(4,y1),
因为AT⊥PF,F(2,0),A(1,0),所以
•
=0,
则(3,y1)•(x-2,y)=0,即3(x-2)+yy1=0,①
因为
•
=0,所以(1-x,-y)•(4-x,y1-y)=0,
即(x-1)(x-4)+y(y-y1)=0,②,
由①②得,x2-2x+y2-2=0,即(x-1)2+y2=3,
所以点P是以A为圆心、
为半径的圆,
则|AP|的长是定值:
;
(2)由题意得,F(2,0)为椭圆E的右焦点,F的最小值为1,最大值为5,
所以c=2,a-c=1,且a+c=5,解得a=3,则b2=9-4=5,
所以椭圆方程是:
+
=1,
设Q(x0,y0)(-3≤x0≤3),则
+
=1,解得y02=5-
,
由(1)知,点P是以A为圆心、
为半径的圆,
所以|PQ|=|AQ|-|AP|=
-
=
-
=
-
,
所以当x0=-
=
时,
取到最小值
,
此时|PQ|取到最小值
-
.
因为AT⊥PF,F(2,0),A(1,0),所以
| AT |
| FP |
则(3,y1)•(x-2,y)=0,即3(x-2)+yy1=0,①
因为
| PA |
| PT |
即(x-1)(x-4)+y(y-y1)=0,②,
由①②得,x2-2x+y2-2=0,即(x-1)2+y2=3,
所以点P是以A为圆心、
| 3 |
则|AP|的长是定值:
| 3 |
(2)由题意得,F(2,0)为椭圆E的右焦点,F的最小值为1,最大值为5,
所以c=2,a-c=1,且a+c=5,解得a=3,则b2=9-4=5,
所以椭圆方程是:
| x2 |
| 9 |
| y2 |
| 5 |
设Q(x0,y0)(-3≤x0≤3),则
| x02 |
| 9 |
| y02 |
| 5 |
| 5x02 |
| 9 |
由(1)知,点P是以A为圆心、
| 3 |
所以|PQ|=|AQ|-|AP|=
| (x0-1)2+y02 |
| 3 |
(x0-1)2+5-
|
| 3 |
=
|
| 3 |
所以当x0=-
| -2 | ||
2×
|
| 9 |
| 4 |
|
| ||
| 2 |
此时|PQ|取到最小值
| ||
| 2 |
| 3 |
点评:本题考查直线、圆、椭圆等知识的综合应用,向量数量积运算和垂直条件,考查运算求解能力和探究能力,函数与方程思想及化归与转化思想.

练习册系列答案
相关题目
已知a∈R,复数z=(a-2i)(1+i)(i为虚数单位)在复平面内对应的点为M,则“a=0”是“点M在第四象限”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若|
|=|
|=|
|=1,且<
,
>=
,则(
+
-
)•(
+
+
)=( )
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
| a |
| b |
| 2 |
| c |
| a |
| b |
| 2 |
| c |
| A、0 | B、1 | C、2 | D、3 |
已知三棱锥的三视图,则该三棱锥的体积是( )
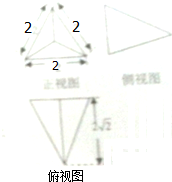

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 将正方体(如图1所示)截去两个三棱锥,得到(如图2所示)的几何体,则该几何体的左视图为( )
将正方体(如图1所示)截去两个三棱锥,得到(如图2所示)的几何体,则该几何体的左视图为( )



 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.