题目内容
平行四边形ABCD中，∠CBA=120°，AD=4，对角线BD=2
，将其沿对角线BD折起，使平面ABD⊥平面BCD，若四面体ABCD顶点在同一个球面上，则该球的体积为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、32
| ||||
| D、2π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离,球
分析：运用余弦定理，可得AB=2，由勾股定理的逆定理可得AB⊥BD，运用面面垂直的性质定理，可得AB⊥BC，
CD⊥AD，再由直角三角形的斜边中线等于斜边的一半，可得球心和半径，再由体积公式计算即可得到．
CD⊥AD，再由直角三角形的斜边中线等于斜边的一半，可得球心和半径，再由体积公式计算即可得到．
解答：
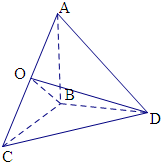解：在△ABD中，BD=2
，AD=4，∠BAD=60°，
由余弦定理可得BD2=AD2+AB2-2AB•ADcos60°，
即为12=16+AB2-4AB，可得AB=2，
由AB2+BD2=AD2，可得AB⊥BD，
由平面ABD⊥平面BCD，则AB⊥平面BCD，
即有AB⊥BC，
由CD⊥BD，平面ABD⊥平面BCD，
则CD⊥平面ABD，
即有CD⊥AD，
取AC的中点O，连接OB，OD，
则有OA=OB=OC=OD=
=
，
即有球的半径r=
．
则球的体积为V=
πr3=
π×（
）3=
π．
故选：A．
解：在△ABD中，BD=2| 3 |
由余弦定理可得BD2=AD2+AB2-2AB•ADcos60°，
即为12=16+AB2-4AB，可得AB=2，
由AB2+BD2=AD2，可得AB⊥BD，
由平面ABD⊥平面BCD，则AB⊥平面BCD，
即有AB⊥BC，
由CD⊥BD，平面ABD⊥平面BCD，
则CD⊥平面ABD，
即有CD⊥AD，
取AC的中点O，连接OB，OD，
则有OA=OB=OC=OD=
| 1 |
| 2 |
| 22+42 |
| 5 |
即有球的半径r=
| 5 |
则球的体积为V=
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 20 |
| 3 |
| 5 |
故选：A．
点评：本题考查面面垂直的性质定理及运用，同时考查勾股定理和直角三角形的性质，考查球的体积公式的运用，属于基础题．
练习册系列答案
相关题目
若|
|=|
|=|
|=1，且＜
，
＞=
，则（
+
-
）•（
+
+
）=（ ）
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
| a |
| b |
| 2 |
| c |
| a |
| b |
| 2 |
| c |
| A、0 | B、1 | C、2 | D、3 |
如图，正方体ABCD-A1B1C1D1中，E为DD1的中点．过原点的直线交双曲线x2-y2=4
于P，Q两点，现将坐标平面沿直线y=-x折成直二面角，则折后PQ长度的最小值等于（ ）
| 2 |
A、2
| ||
| B、4 | ||
C、4
| ||
D、3
|
已知三棱锥的三视图，则该三棱锥的体积是（ ）
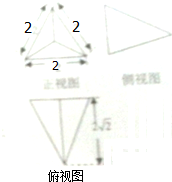
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若实数a，b，c满足a2+b2+c2=1，则3ab-3bc+2c2的最大值为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知圆的方程为（x-t）2+（y-t-1）2=2（t∈[-2，2]），则它的圆心的轨迹方程为（ ）
| A、x-y+1=0，x∈[-2，2] |
| B、x+y+1=0，x∈[-2，2] |
| C、x-y-1=0，x∈[-2，2] |
| D、x+y-1=0，x∈[-2，2] |