题目内容
已知不等式
≤6对?x∈R恒成立，则实数p的值为 ．
| 3x2+px+6 |
| x2-x+1 |
考点：函数恒成立问题
专题：函数的性质及应用
分析：注意到所给的不等式分母为正，因此可以将问题转化为一元二次不等式恒成立问题，借助于二次函数的知识不难解决．
解答：
解：
≤6对?x∈R恒成立，结合x2-x+1=(x-
)2+
＞0恒成立，
故原式可化为3x2-（p+1）x≥0对一切x∈R恒成立．
则只需△=（p+1）2≤0即可．
故p+1=0，即p=-1．
| 3x2+px+6 |
| x2-x+1 |
| 1 |
| 2 |
| 3 |
| 4 |
故原式可化为3x2-（p+1）x≥0对一切x∈R恒成立．
则只需△=（p+1）2≤0即可．
故p+1=0，即p=-1．
点评：本题充分注意到分母大于零恒成立，从而将问题转化为一元二次不等式的恒成立问题是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数A={x|y=cos（
）}，B={y|y=tanx，x∈[-
，
]}，则A∩B=（ ）
| 1 |
| x+1 |
| π |
| 4 |
| π |
| 4 |
| A、∅ |
| B、{x|x≠-1} |
| C、{x|-1≤x≤1} |
| D、{x|-1＜x≤1} |
已知三棱锥S-ABC的体积为V，D，E，F，分别是棱SB，BC，SC的中点，三棱锥A-DEF体积为V1，则
=（ ）
| V1 |
| V |
A、
| ||
B、
| ||
C、
| ||
D、
|
若|
|=|
|=|
|=1，且＜
，
＞=
，则（
+
-
）•（
+
+
）=（ ）
| a |
| b |
| c |
| a |
| b |
| π |
| 2 |
| a |
| b |
| 2 |
| c |
| a |
| b |
| 2 |
| c |
| A、0 | B、1 | C、2 | D、3 |
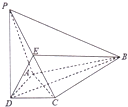如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD⊥DC，DB平分∠ADC，E为PC的中点，AD=CD=1，DB=2