题目内容
求值
(1)sin105°;
(2)cosα=
,求cos2α的值.
(1)sin105°;
(2)cosα=
| ||
| 2 |
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:(1)sin105°=sin(60°+45°)再由两角和的正弦公式和特殊角的三角函数值,即可得到;
(2)运用二倍角的余弦公式cos2α=2cos2α-1,即可得到.
(2)运用二倍角的余弦公式cos2α=2cos2α-1,即可得到.
解答:
解:(1)sin105°=sin(60°+45°)
=sin60°cos45°+cos60°sin45°
=
×
+
×
=
;
(2)cos2α=2cos2α-1
=2×(
)2-1=1-1=0.
=sin60°cos45°+cos60°sin45°
=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
(2)cos2α=2cos2α-1
=2×(
| ||
| 2 |
点评:本题考查三角函数的求值,考查两角和的正弦公式和二倍角的余弦公式,考查运算能力,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.
如图,在Rt△ABC中,∠ACB=90°,|BC|=4,|AC|=3,一曲线E过点A,动点P在曲线E运动,且保持|PC|+|PB|的值不变.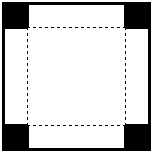 如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?