题目内容
6个人站成一列排队,求:
(1)甲、乙相邻,有几种排法?
(2)甲、乙不相邻,有几种排法?
(3)甲不排头,乙不排尾,有几种排法?
(1)甲、乙相邻,有几种排法?
(2)甲、乙不相邻,有几种排法?
(3)甲不排头,乙不排尾,有几种排法?
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)相邻问题,采用捆绑法.先排甲、乙,再与其他4名同学排列,问题得以解决.
(2)不相邻问题,采用插空法,先排其余的4名同学,出现5个空,将甲、乙插空,问题得以解决,
(3)分两类,乙在排头有
;乙不排头有
,根据分类计数原理即可得到答案.
(2)不相邻问题,采用插空法,先排其余的4名同学,出现5个空,将甲、乙插空,问题得以解决,
(3)分两类,乙在排头有
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
解答:
解:(1)采用捆绑法.先排甲、乙,有
种方法,再与其他4名同学排列,共有
•
=240种不同排法,
(2)采用插空法先排其余的4名同学,有
种排法,出现5个空,将甲、乙插空,所以共有
•
=480种不同排法,
(3)分两类,乙在排头有
;乙不排头有
,根据分类计数原理得
+
=504种不同排法.
| A | 2 2 |
| A | 2 2 |
| A | 5 5 |
(2)采用插空法先排其余的4名同学,有
| A | 4 4 |
| A | 4 4 |
| A | 2 5 |
(3)分两类,乙在排头有
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
点评:本题主要考查了排列问题中的几种常用方法,相邻用捆绑面部相邻与插空,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
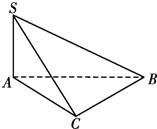 如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2
如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2