题目内容
在某校组织的一次篮球定点投篮测试中,规定每人最多投3次,每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于DE分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投;方案2:都在P处投篮.甲同学在AD1E处投篮的命中率为
,在B处投篮的命中率为0.8.
(Ⅰ)甲同学选择方案1.①求甲同学测试结束后所得总分等于4的概率;②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
| ||
| 3 |
(Ⅰ)甲同学选择方案1.①求甲同学测试结束后所得总分等于4的概率;②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)①在A处投篮命中记作A,不中记作
;在B处投篮命中记作B,不中记作
;甲同学测试结束后所得总分为4可记作事件
BB,由此能求出甲同学测试结束后所得总分等于4的概率.
②ξ的所有可能取值为0,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
(Ⅱ)甲同学选择方案1通过测试的概率为P1,选择方案2通过测试的概率为P2,分别求出p1,p2,由此得到甲同学应选择方案2通过测试的概率更大.
. |
| A |
. |
| B |
. |
| A |
②ξ的所有可能取值为0,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
(Ⅱ)甲同学选择方案1通过测试的概率为P1,选择方案2通过测试的概率为P2,分别求出p1,p2,由此得到甲同学应选择方案2通过测试的概率更大.
解答:
20.(本小题满分12分)
解:(Ⅰ)①在A处投篮命中记作A,不中记作
;
在B处投篮命中记作B,不中记作
;
甲同学测试结束后所得总分为4可记作事件
BB,
则P(
BB)=P(
)P(B)P(B)=0.5×0.8×0.8=0.32…(2分)
②ξ的所有可能取值为0,2,3,4,
P(ξ=2)=P(
B
)+P(
B)=P(
)P(B)P(
)+P(
)P(
)P(B)
=0.5×0.8×(1-0.8)+0.5×(1-0.8)×0.8=0.16,
P(ξ=3)=P(A)=0.5,
P(ξ=4)=P(
BB)=P(
)P(B)P(B)=0.5×0.8×0.8=0.32,
P(ξ=0)=1-0.16-0.5-0.32=0.02,…(6分)
∴ξ的分布列为:
Eξ=0×0.02+2×0•16+3×0.5+4×0.32=3.1.
(Ⅱ)甲同学选择方案1通过测试的概率为P1,
选择方案2通过测试的概率为P2,
P1=P(ξ≥3)=0.5+0.32=0.82,
P2=P(
BB)+P(B
B)+P(BB)=2×0.8×0.2+0.8×0.8=0.896,
∵P2>P2,
∴甲同学应选择方案2通过测试的概率更大.
解:(Ⅰ)①在A处投篮命中记作A,不中记作
. |
| A |
在B处投篮命中记作B,不中记作
. |
| B |
甲同学测试结束后所得总分为4可记作事件
. |
| A |
则P(
. |
| A |
. |
| A |
②ξ的所有可能取值为0,2,3,4,
P(ξ=2)=P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
. |
| A |
. |
| B |
=0.5×0.8×(1-0.8)+0.5×(1-0.8)×0.8=0.16,
P(ξ=3)=P(A)=0.5,
P(ξ=4)=P(
. |
| A |
. |
| A |
P(ξ=0)=1-0.16-0.5-0.32=0.02,…(6分)
∴ξ的分布列为:
| ξ | 0 | 2 | 3 | 4 |
| P | 0.02 | 0.16 | 0.5 | 0.32 |
(Ⅱ)甲同学选择方案1通过测试的概率为P1,
选择方案2通过测试的概率为P2,
P1=P(ξ≥3)=0.5+0.32=0.82,
P2=P(
. |
| B |
. |
| B |
∵P2>P2,
∴甲同学应选择方案2通过测试的概率更大.
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
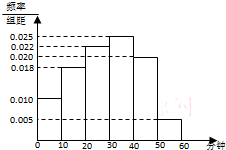 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图; 将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图; 将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”