题目内容
函数y=sinx+
cosx，x∈[-
，
]的值域是 ．
| 3 |
| 2π |
| 3 |
| π |
| 3 |
考点：三角函数的最值
专题：三角函数的图像与性质
分析：利用三角函数的辅助角公式将函数进行化简，利用三角函数的图象和性质即可得到结论．
解答：
解：y=sinx+
cosx=2sin（x+
），
若x∈[-
，
]，
则x+
∈[-
，
]，
则-
≤sin（x+
）≤1，
即-
≤2sin（x+
）≤2，
∴函数的值域为[-
，2]，
故答案为：[-
，2]．
| 3 |
| π |
| 3 |
若x∈[-
| 2π |
| 3 |
| π |
| 3 |
则x+
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
则-
| ||
| 2 |
| π |
| 3 |
即-
| 3 |
| π |
| 3 |
∴函数的值域为[-
| 3 |
故答案为：[-
| 3 |
点评：本题主要考查三角函数的图象和性质，利用辅助角公式将函数进行化简是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
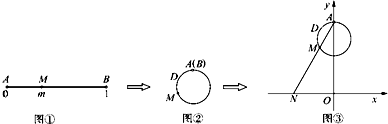如图展示了一个由区间（0，1）到实数集R的映射过程：区间（0，1）中的实数m对应数轴上的点M，如图①；将线段AB围成一个圆，使两端点A、B恰好重合，如图②；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），在图形变化过程中，图①中线段AM的长度对应于图③中的弧ADM的长度，如图③．图③中直线AM与x轴交于点N（n，0），则m的象就是n，记作f（m）=n．在△ABC中，点M是BC中点．若∠A=120°，
•
=-
，则|
|的最小值是（ ）
| AB |
| AC |
| 1 |
| 2 |
| AM |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列关于极限的计算，错误的是（ ）
A、
| ||||||||||||||||||||
B、
| ||||||||||||||||||||
C、
| ||||||||||||||||||||
D、已知an=
|