题目内容
已知直线l⊥平面α,直线m?平面β,则下列四个命题中,真命题是( )
| A、l∥m⇒α⊥β |
| B、α⊥β⇒l∥m |
| C、l⊥m⇒α∥β |
| D、l⊥m⇒α⊥β |
考点:平面与平面之间的位置关系,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用直线与直线,直线与平面,平面与平面的位置关系逐一判断,成立的证明,不成立的可举出反例.
解答:
解:∵l⊥α,l∥m,∴m⊥α,又∵m?β,∴α⊥β,故A为真命题.
若α⊥β,l⊥α,则l∥β或l?β,又∵m?β,∴l与m可能平行也可能相交,也可能异面,故B为假命题.
若l⊥m,l⊥α,则m∥α或m?α,又由m?β,则α与β可能平行,可能相交,位置不确定,故C为假命题;
若l⊥m,l⊥α,则m∥α或m?α,又由m?β,则α与β可能平行,可能相交,位置不确定,故D为假命题
故选A
若α⊥β,l⊥α,则l∥β或l?β,又∵m?β,∴l与m可能平行也可能相交,也可能异面,故B为假命题.
若l⊥m,l⊥α,则m∥α或m?α,又由m?β,则α与β可能平行,可能相交,位置不确定,故C为假命题;
若l⊥m,l⊥α,则m∥α或m?α,又由m?β,则α与β可能平行,可能相交,位置不确定,故D为假命题
故选A
点评:本题主要考查显现,线面,面面位置关系的判断,属于概念题.

练习册系列答案
相关题目
函数y=2-
的值域是( )
| -x2+4x |
| A、[-2,2] | ||||
| B、[1,2] | ||||
| C、[0,2] | ||||
D、[-
|
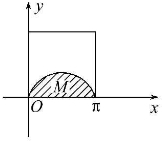 如图,在边长为π的正方形内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往正方形内投一个点P,则点P落在区域M内的概率是( )
如图,在边长为π的正方形内的正弦曲线y=sinx与x轴围成的区域记为M(图中阴影部分),随机往正方形内投一个点P,则点P落在区域M内的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知AB为圆O的一条弦,且|AB|=2,则数量积
•
的值为( )
| AB |
| AO |
| A、2 | B、3 |
| C、4 | D、与圆的半径有关 |
设集合M={x|x<2012},N={x|0<x≤2012},则M∪N=( )
| A、M |
| B、N |
| C、{x|x≤2012} |
| D、{x|0<x<2012} |
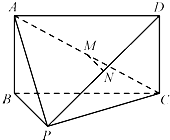 如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.求证:
如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.求证: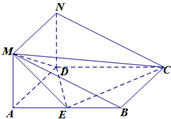 如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.
如图所示的几何体中,四边形ABCD为菱形,AMND是矩形,平面AMND⊥平面ABCD,∠DAB=60°,AD=2,AM=1.