题目内容
等差数列{an}的前三项为5,8,11,等差数列{bn}的前三项为3、7、11,它们的项数均为100,则这两个数列中共有多少个相同的项?
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:等差数列{an}的公差是3,最后一项是302;等差数列{bn}的公差是4,最后一项是399,所以共同项组成的数列cn的公差是12,首项为11.再结合11+12(x-1)≤302,可得结论.
解答:
解:等差数列{an}的公差是3,最后一项是302;等差数列{bn}的公差是4,最后一项是399,
所以共同项组成的数列{cn}的公差是12,首项为11.
由11+12(x-1)≤302,可得x=25,所以一共25个相同项.
所以共同项组成的数列{cn}的公差是12,首项为11.
由11+12(x-1)≤302,可得x=25,所以一共25个相同项.
点评:本题考查等差数列的性质,考查学生分析解决问题的能力,确定共同项组成的数列{cn}的公差是12,首项为11是关键.

练习册系列答案
相关题目
已知直线l⊥平面α,直线m?平面β,则下列四个命题中,真命题是( )
| A、l∥m⇒α⊥β |
| B、α⊥β⇒l∥m |
| C、l⊥m⇒α∥β |
| D、l⊥m⇒α⊥β |
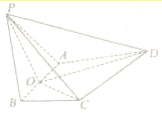 已知四棱锥p-ABCD中,面PAB⊥面ABCD,且BC∥AD,BC⊥AB,且PA=PB=4,AB=2,BC=1,AD=3,O为AB的中点.
已知四棱锥p-ABCD中,面PAB⊥面ABCD,且BC∥AD,BC⊥AB,且PA=PB=4,AB=2,BC=1,AD=3,O为AB的中点.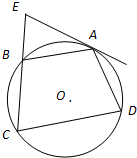 如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.
如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.