题目内容
函数y=2-
的值域是（ ）
| -x2+4x |
| A、[-2，2] | ||||
| B、[1，2] | ||||
| C、[0，2] | ||||
D、[-
|
考点：函数的值域
专题：计算题,函数的性质及应用
分析：确定t=-x2+4x的范围，即可求出函数y=2-
的值域．
| -x2+4x |
解答：
解：令t=-x2+4x=-（x-2）2+4，则t≤4，
∴0≤
≤2
∴-2≤-
≤0，
∴0≤2-
≤2，
∴函数y=2-
的值域是[0，2]．
故选：C．
∴0≤
| -x2+4x |
∴-2≤-
| -x2+4x |
∴0≤2-
| -x2+4x |
∴函数y=2-
| -x2+4x |
故选：C．
点评：本题考查函数的值域，考查学生的计算能力，比较基础．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
在空间中，下列正确命题的个数是（ ）
①若
•
=0，则
=0或
=0；
②（
•
）
=
（
•
）；
③
2
2=（
•
）2；
④|
+
||
-
|=|
-
|；
⑤
与（
•
）
-（
•
）
垂直．
①若
| a |
| b |
| a |
| b |
②（
| a |
| b |
| c |
| a |
| b |
| c |
③
| p |
| q |
| p |
| q |
④|
| p |
| q |
| p |
| q |
| p |
| q |
⑤
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| A、1 | B、2 | C、3 | D、4 |
下列函数的值域为[1，+∞）的是（ ）
A、y=（
| ||
B、y=（
| ||
| C、y=log2（x2-2x+2） | ||
| D、y=log2（x2-2x+3） |
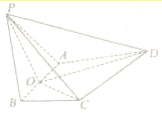已知四棱锥p-ABCD中，面PAB⊥面ABCD，且BC∥AD，BC⊥AB，且PA=PB=4，AB=2，BC=1，AD=3，O为AB的中点．已知直线l⊥平面α，直线m?平面β，则下列四个命题中，真命题是（ ）
| A、l∥m⇒α⊥β |
| B、α⊥β⇒l∥m |
| C、l⊥m⇒α∥β |
| D、l⊥m⇒α⊥β |